第 2 节 树形问题

第 2 节到第 4 节以「力扣」第 46 题为例，深入讲解「回溯算法」。

在树形问题中使用深度优先遍历

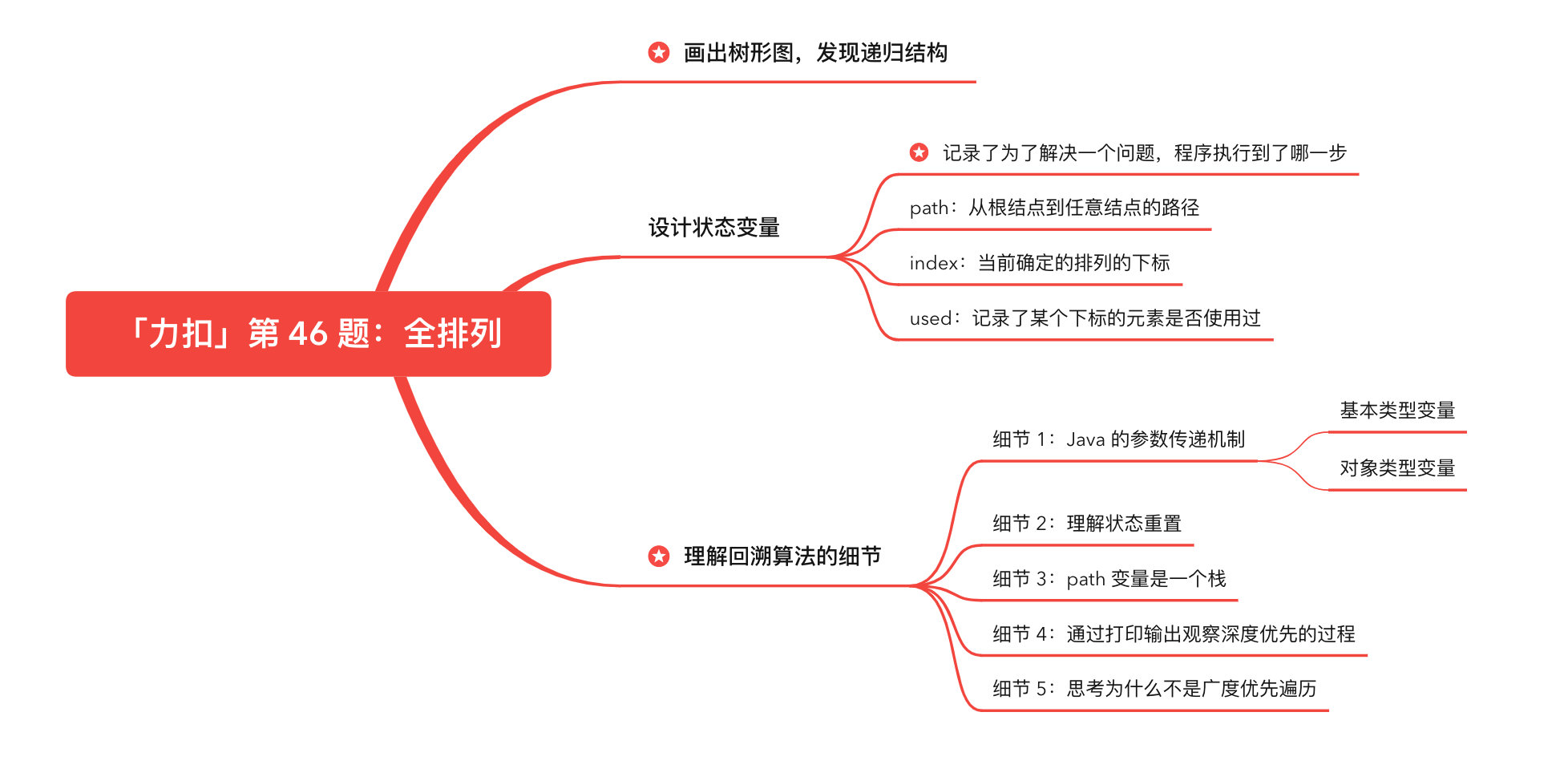
例题：「力扣」第 46 题：全排列

• 题目链接 (opens new window)
• 题解链接 (opens new window)

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

解题思路

我们尝试在纸上写 个数字、 个数字、 个数字的全排列，相信不难找到这样的方法。以数组 [1, 2, 3] 的全排列为例。

• 先写以 开头的全排列，它们是：[1, 2, 3], [1, 3, 2]，即 1 + [2, 3] 的全排列（注意：递归结构体现在这里）；
• 再写以 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]，即 2 + [1, 3] 的全排列；
• 最后写以 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]，即 3 + [1, 2] 的全排列。

总结搜索的方法：按顺序枚举每一位可能出现的情况，已经选择的数字在 当前 要选择的数字中不能出现。按照这种策略搜索就能够做到 不重不漏。这样的思路，可以用一个树形结构表示。

看到这里的朋友，建议先尝试自己画出「全排列」问题的树形结构。

说明：

• 每一个结点表示了求解全排列问题的不同的阶段，这些阶段通过变量的「不同的值」体现，这些变量的不同的值，称之为「状态」；
• 使用深度优先遍历有「回头」的过程，在「回头」以后， 状态变量需要设置成为和先前一样 ，因此在回到上一层结点的过程中，需要撤销上一次的选择，这个操作称之为「状态重置」；
• 深度优先遍历，借助系统栈空间，保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候，状态变量的值是正确的，具体的做法是：往下走一层的时候，path 变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此 path 变量是一个栈；
• 深度优先遍历通过「回溯」操作，实现了全局使用一份状态变量的效果。

使用编程的方法得到全排列，就是在这样的一个树形结构中完成 遍历，从树的根结点到叶子结点形成的路径就是其中一个全排列。

设计状态变量

• 首先这棵树除了根结点和叶子结点以外，每一个结点做的事情其实是一样的，即：在已经选择了一些数的前提下，在剩下的还没有选择的数中，依次选择一个数，这显然是一个 递归 结构；
• 递归的终止条件是： 一个排列中的数字已经选够了 ，因此我们需要一个变量来表示当前程序递归到第几层，我们把这个变量叫做 depth，或者命名为 index ，表示当前要确定的是某个全排列中下标为 index 的那个数是多少；
• 布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。

这些变量称为「状态变量」，它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。

代码实现

参考代码 1：

注意：下面的代码是错误的，希望读者能运行测试用例，发现原因，然后再阅读后面的内容。

Java 代码：

import java.util.ArrayList;
import java.util.List;

public class Solution {

    public List<List<Integer>> permute(int[] nums) {
        int len = nums.length;
        // 使用一个动态数组保存所有可能的全排列
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        boolean[] used = new boolean[len];
        List<Integer> path = new ArrayList<>();

        dfs(nums, len, 0, path, used, res);
        return res;
    }

    private void dfs(int[] nums, int len, int depth,
                     List<Integer> path, boolean[] used,
                     List<List<Integer>> res) {
        if (depth == len) {
            res.add(path);
            return;
        }

        // 在非叶子结点处，产生不同的分支，这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。
        for (int i = 0; i < len; i++) {
            if (!used[i]) {
                path.add(nums[i]);
                used[i] = true;

                dfs(nums, len, depth + 1, path, used, res);
                // 注意：下面这两行代码发生 「回溯」，回溯发生在从 深层结点 回到 浅层结点 的过程，代码在形式上和递归之前是对称的
                used[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        Solution solution = new Solution();
        List<List<Integer>> lists = solution.permute(nums);
        System.out.println(lists);
    }

}

Python 代码：

from typing import List


class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def dfs(nums, size, depth, path, used, res):
            if depth == size:
                res.append(path)
                return

            for i in range(size):
                if not used[i]:
                    used[i] = True
                    path.append(nums[i])

                    dfs(nums, size, depth + 1, path, used, res)

                    used[i] = False
                    path.pop()

        size = len(nums)
        if len(nums) == 0:
            return []

        used = [False for _ in range(size)]
        res = []
        dfs(nums, size, 0, [], used, res)
        return res


if __name__ == '__main__':
    nums = [1, 2, 3]
    solution = Solution()
    res = solution.permute(nums)
    print(res)

执行 main 方法以后输出如下：

[[], [], [], [], [], []]

原因出现在 递归终止条件 这里：

Java 代码：

if (depth == len) {
    res.add(path);
    return;
}

Python 代码：

if depth == size:
    res.append(path)
    return

变量 path 所指向的列表 在深度优先遍历的过程中只有一份 ，深度优先遍历完成以后，回到了根结点，成为空列表。

在 Java 中，参数传递是 值传递，对象类型变量在传参的过程中，复制的是变量的地址。这些地址被添加到 res 变量，但实际上指向的是同一块内存地址，因此我们会看到 个空的列表对象。解决的方法很简单，在 res.add(path); 这里做一次拷贝即可。

修改的部分：

Java 代码：

if (depth == len) {
    res.add(new ArrayList<>(path));
    return;
}

Python 代码：

if depth == size:
    res.append(path[:])
    return

此时再提交到「力扣」上就能得到通过了，完整代码请见下文「参考代码 2」。

复杂度分析：

提示：「回溯算法」的复杂度分析理论性很强，初学回溯算法的时候可以暂时跳过。

回溯算法由于其遍历的特点，时间复杂度一般都比较高，有些问题分析起来很复杂。一些回溯算法解决的问题，剪枝剪得好的话，复杂度会降得很低，因此分析最坏时间复杂度的意义也不是很大。但还是视情况而定。

• 时间复杂度：

非叶子结点的个数，依次为（按照层数来）：

$$ 1 + A_N^1 + A_N^2 + \cdots + A_N^{N-1} = 1 + \cfrac{N!}{(N - 1)!} + \cfrac{N!}{(N - 2)!} + \cdots + N! $$

说明：根结点为 ，计算复杂度的时候忽略； 表示排列数，计算公式为 。

在第 1 层，结点个数为 个数选 1 个的排列，故为 ；

在第 2 层，结点个数为 个数选 2 个的排列，故为 。

$$ \cfrac{N!}{(N - 1)!} + \cfrac{N!}{(N - 2)!} + \cdots + N! = N! \left( \cfrac{1}{(N - 1)!} + \cfrac{1}{(N - 2)!} + \cdots + 1 \right) \le N! \left( 1 + \cfrac{1}{2} + \cfrac{1}{4} + \cdots + \cfrac{1}{2^{N - 1}} \right) < 2N! $$

将常系数 视为 ，每个内部结点循环 次，故非叶子结点的时间复杂度为 ；

最后一层共 个叶节点，在叶子结点处拷贝需要 ，叶子结点的时间复杂度也为 。

• 空间复杂度：。
  • 递归树深度 ；
  • 全排列个数 ，每个全排列占空间 。取较大者。

参考资料

• liuyubobobo 老师在慕课网上开设的课程《玩转算法面试》代码仓库 (opens new window)。

---

作者：liweiwei1419 链接：https://suanfa8.com/backtracking/tree 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。