# 第 8 节三种二分查找模板对比

我知道二分查找常见有 3 种写法，是在「力扣」的「学习」板块的「LeetBook」里，有一本叫「二分查找」的 LeetBook。

如果你使用英文版的 LeetCode，「学习」版块叫「explore」。

我简单解释一下大家常见的三个模板，它们区分的标志是 while 里面写什么。

模板 1：while (left <= right)
模板 2：while (left < right)
模板 3：while (left + 1 < right)

# 模板 1：`while (left <= right)`

看到 while (left <= right) 这种写法的朋友们，你一定会看到「大佬」们这么用：声明一个 ans 变量，一定会出现在 if 和 else 分支里的其中一个。

以下是「力扣」第 35 题官方题解：

题目要我们找的是：第 1 个大于等于 target 的元素的位置，当看到一个元素 nums[mid] 大于等于 target 的时候，nums[mid] 有可能就是我们要找的，所以把 ans 先保存为 mid；
数组的长度 n ，也就是数组的最后一个元素的下一个位置也有可能是答案，所以一开始的时候设置 ans = n；
if 和 else 里面，不管怎么样，left 和 right 的设置都需要 + 1 或者 -1。设置 left = mid + 1，说明下一轮向右边找，设置 right = mid - 1 ，说明下一轮向左边找。这是因为：mid 如果有可能是解的话，因为有了 ans 的设置，一定不会丢失最优解；
当 left == right 重合的时候，left 位置的值还没有看到，所以要继续找下去，因此循环可以继续的条件是 while (left <= right)；
最后返回的是 ans 哦，不是 left 或者 right 的任何一个。

大家可以在回头看看本章第 2 节（标题为：「力扣」上一类问题的特点（极其重要）），我复制下来，重要的事情讲 3 遍。

提示：如果当前猜的那个数 nums[mid] 符合某个性质，我们还不能确定它一定就是我们要找的元素，必须向左边（或者向右边）继续看下去，才能确定 nums[mid] 是不是我们要找的元素。

这种写法也叫带 ans 的「二分查找」，「力扣」的巨佬：零神（id：zerotrac）以前就经常用这种写法，现在我不刷题了，所以不知道他是不是还这样写。

# 模板 2：`while (left < right)`

如果你看过我在第 35 题写的题解，就会知道我一直在用这种写法，所以我这里就不展开了。简单说一下：

while (left < right) 这种写法，我最喜欢的地方是退出循环以后 left 与 right 重合；
这种写法我起过很多名字：「两边夹」、「排除法」。它看起来像下面这个样子：

叫「两边夹」是因为这个写法是：两个变量 left 和 right 向中间走，相遇的时候停下。相遇的时候是 left == right，所以循环可以继续的条件是 while (left < right)。

叫「排除法」是每一轮都把一定不是目标元素的值排除掉，下一轮只在有可能存在目标元素的区间里查找。

这种写法最难理解的地方是当看到 left = mid 的时候，取中间数需要加。原因在于：整数除法是下取整，取 mid 的时候不能做到真正取到中间位置，例如 left = 3, right = 4， mid = (left + right) / 2 = 3，此时 mid 的值等于 left，一旦进入 left = mid 这个分支，搜索区间不能缩小，因此会进入死循环。

这是很多朋友和我说最难理解的地方，我有两个办法：

办法 1：遇到死循环的时候，把 left、right、mid 的值打印出来看一下，例如「力扣」第 69 题。

public class Solution {

    public int mySqrt(int x) {
        // 特殊值判断
        if (x == 0) {
            return 0;
        }
        if (x == 1) {
            return 1;
        }

        int left = 1;
        int right = x / 2;
        // 在区间 [left..right] 查找目标元素
        while (left < right) {
            // 取中间数 mid 下取整时
            int mid = left + (right - left ) / 2;

            // 调试语句开始
            try {
                Thread.sleep(1000);
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
            System.out.println("left = " + left + ", right = " + right + ", mid = " + mid);
            // 调试语句结束

            // 注意：这里为了避免乘法溢出，改用除法
            if (mid > x / mid) {
                // 下一轮搜索区间是 [left..mid - 1]
                right = mid - 1;
            } else {
                // 下一轮搜索区间是 [mid..right]
                left = mid;
            }
        }
        return left;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int x = 9;
        int res = solution.mySqrt(x);
        System.out.println(res);
    }
}

提示：这里有个小技巧，我一般会在注释里写上「下一轮搜索区间是什么」。如果下一轮搜索区间是 [mid..right] ，这个时候就设置 left = mid，这种情况的反面区间就是 [left..mid - 1] ，那么 else 就设置 right = mid - 1。区间 [mid..right] 和 [left..mid - 1] 组成了原来的整个区间 [left..right] 不用记忆配对关系了。

办法 2：暂时不用管这件事情，题目做多了，就慢慢理解了。

「力扣」上很多大佬用的都是这种写法，例如宫水三叶（id：ac_oier），张晴川（id：qingczha）。

这种写法需要注意的地方：

看到 mid 的时候一定要清楚两件事情：

mid 是不是解；
下一轮向左边找，还是向右边找。

所以就会有「left = mid 与 right = mid - 1」与「left = mid + 1 与 right = mid」这两种区间设置，其实就是一个包含 mid 一个不包含 mid 的区别而已。

分成两个区间，如果分成三个区间，不一定退出循环以后 left 与 right 会重合。

怎么知道 mid 是不是解，下一轮向左边找，还是向右边找，答案是：看题目，重要的事情说三遍，看题目、看题目、看题目。

所以这里还有一个小技巧：分析清楚题目要找的元素需要符合什么性质。

if 写不符合这个性质，把 mid 排除掉；
else 就恰好是这个性质。

原因很简单：不符合性质的时候，把 mid 排除掉的逻辑不容易出错（这是个人感觉，评论区有和我一样有同感的朋友）。但是这一点不绝对，我做过的题目只有「力扣」第 287 题例外。

例如「力扣」第 35 题：题目要我们找：第一个大于等于 target 的元素的位置。

所以如果看到的元素 nums[mid] 的值 严格小于 target，mid 肯定不是我们要找的，下一轮应该在右边继续查找，所以下一轮搜索区间是 [mid + 1..right]，设置 left = mid = 1，下面的代码 if 就是这么写出来的。

public class Solution {

    public int searchInsert(int[] nums, int target) {
        int len = nums.length;
        int left = 0;
        int right = len;
        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] < target) {
                // 下一轮搜索区间是 [mid + 1..right]
                left = mid + 1;
            } else {
                // 下一轮搜索区间是 [left..mid]
                right = mid;
            }
        }
        return left;
    }
}

其它细节，由于篇幅的原因就不解释了。大家题目做多了，都能理解到。

# 模板 3：`while (left + 1 < right)`

下面这段代码是我从 LeetBook 里面截图，把需要注意的地方加上了注释。

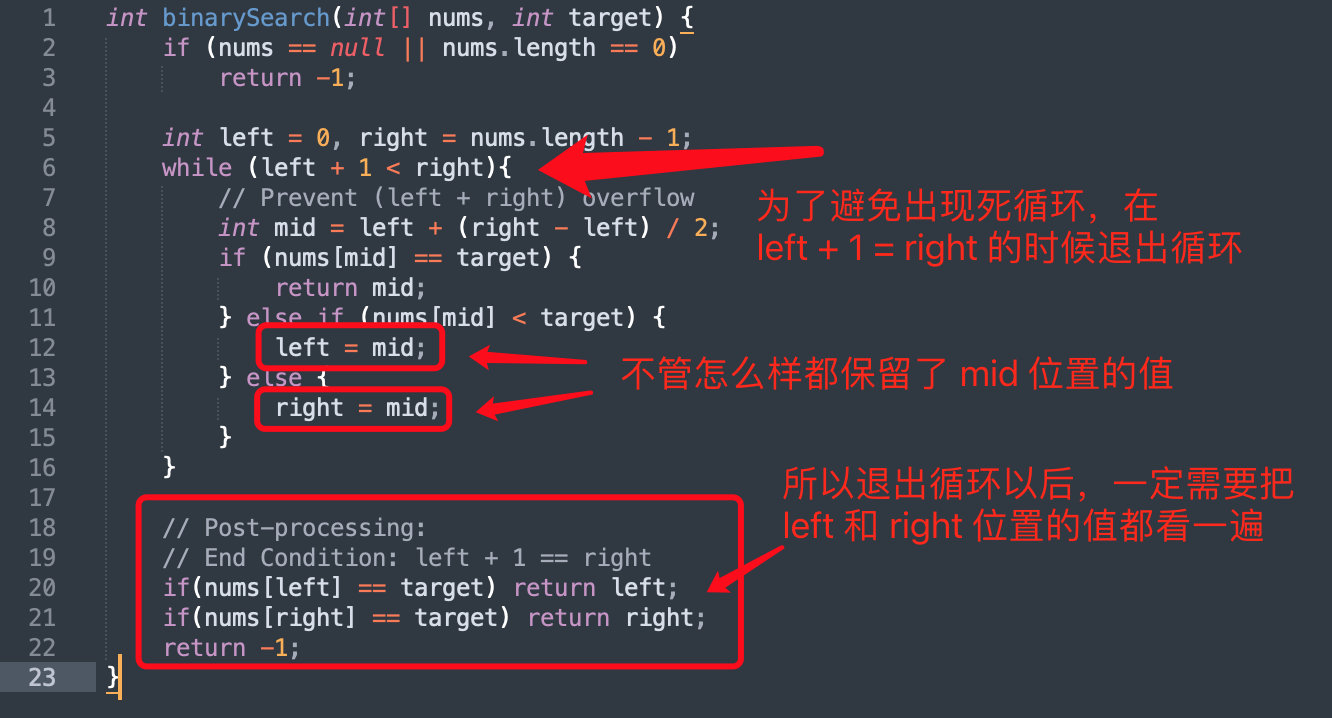
这种写法的提出者我也不知道是谁，我看蛮多人爱用这种写法的。设计这种写法的想法（好处）和不好的地方，我为大家罗列一下。

为了不想判断 mid 是不是保留，把 left 和 right 的设置都写成：left = mid 和 right = mid。表示的意思是都保留了 mid 位置的值，但是不能省去的判断是「下一轮向左走还是向右走」；
为了不想出现死循环，把循环可以继续的条件写成了 while (left + 1 < right)，但是不能省去的判断是「退出循环以后」，一定要再判断一下 left 和 right 哪一个才是题目要找的解，这一步有可能会增加一些本来不必要的逻辑（例如「力扣」第 34 题）。

# 我用什么模板

我不固定用哪一种写法，绝大多数情况用「模板二」，这是因为「力扣」上很多问题都是较为复杂的问题，绝对不用「模板三」，模板三就是在背代码，然后往里面填空，事实上没有必要这么做。

怎么写「二分查找」，依然是得看问题问的是什么：

如果要找的元素性质简单，可以在循环体内决定，我写成 while (left <= right)，并且不设置 ans，因为循环体内就可以返回，没有必要设置 ans；
如果要找的元素性质稍微复杂，就需要要在退出循环体以后决定，我写成 while (left < right)，因为只要仔细的判断，完全可以清楚 mid 是否排除和下一轮向左边走还是向右边走。出现死循环的原因和解决办法我已经完全理解。我写的题解绝大多数都是这种写法，并且「力扣」上的问题绝大多数都是下面这类问题：

提示：重要的事情说三遍，这是本文第三次出现了如果当前猜的那个数 nums[mid] 符合某个性质，我们还不能确定它一定就是我们要找的元素，必须向左边（或者向右边）继续看下去，才能确定 nums[mid] 是不是我们要找的元素。

因此其实重点在 if 和 else 怎么写，再强调一下这个小技巧：分析清楚题目要找的元素需要符合什么性质。

if 写不符合这个性质，把 mid 排除掉；
else 就恰好是这个性质。

# 总结

「二分查找」的确是有很多需要细心的地方，但它不是完全不能掌握的，大家需要有一些耐心，题目做得多了，慢慢就理解了。

作者：liweiwei1419 链接：https://suanfa8.com/binary-search/template-comparison 来源：算法吧著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

← 第 7 节 while (left < right) 一定表示左闭右开吗？第 9 节写对「二分查找」的经验 →

# 第 8 节 三种二分查找模板对比

# 模板 1：while (left <= right)

# 模板 2：while (left < right)