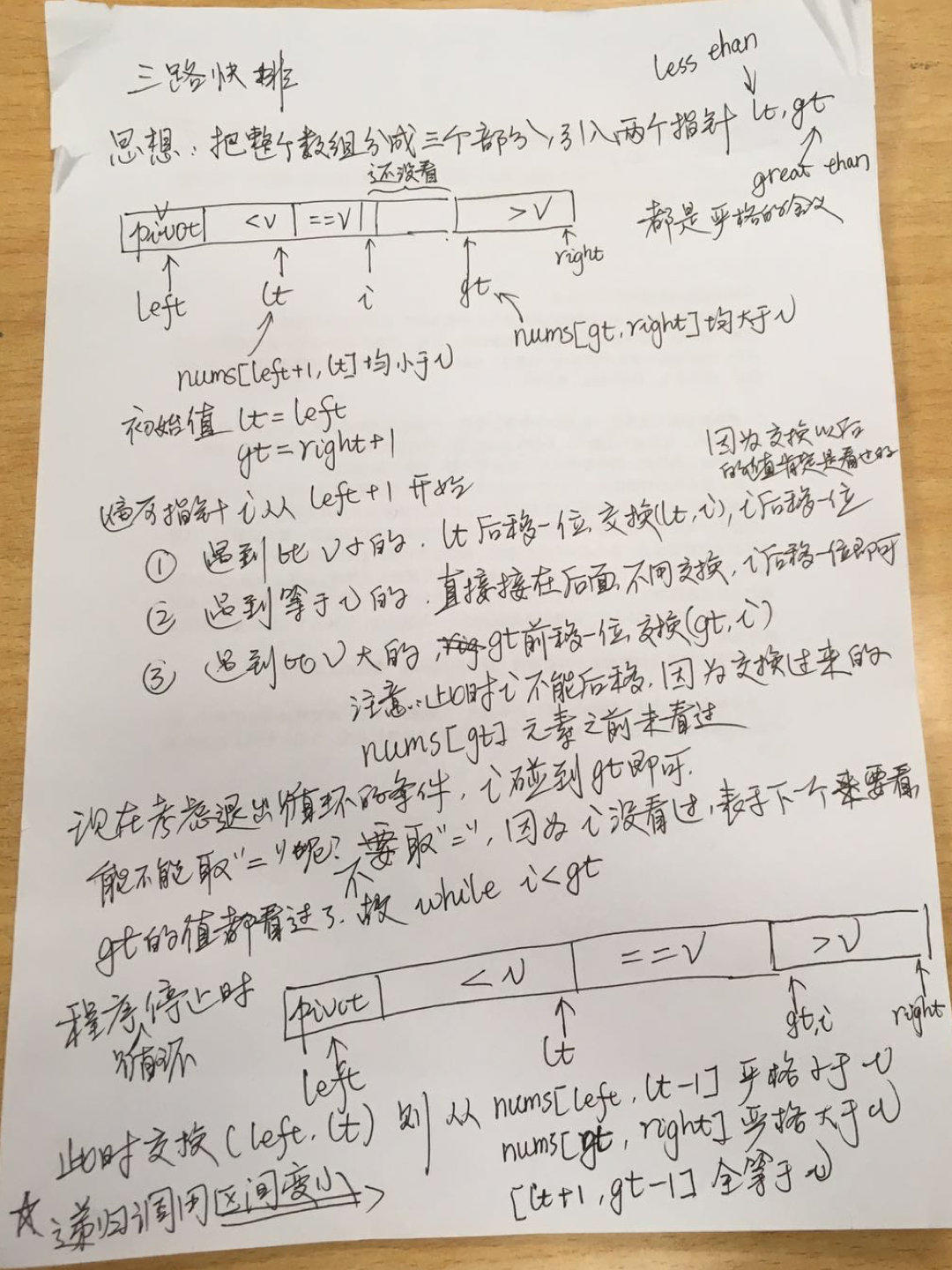
# 第 6 节 三路快排
# 视频讲解
建议快进播放。
参考代码 1:
import java.util.Random;
class Solution {
private final static Random random = new Random(System.currentTimeMillis());
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
// [left..right]
int randomIndex = left + random.nextInt(right - left + 1);
swap(nums, left, randomIndex);
int pivot = nums[left];
int lt = left + 1; // lt: less than
int gt = right; // ge: greater than
// all in nums[left + 1..lt) < pivot
// all in nums[lt..i) = pivot
// all in nums(gt..right] > pivot
int i = left + 1;
while (i <= gt) {
if (nums[i] < pivot) {
swap(nums, i, lt);
lt++;
i++;
} else if (nums[i] == pivot) {
i++;
} else {
// nums[i] > pivot
swap(nums, i, gt);
gt--;
}
}
swap(nums, left, lt - 1);
quickSort(nums, left, lt - 2);
quickSort(nums, gt + 1, right);
}
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
修改定义。
参考代码 2:
import java.util.Random;
class Solution {
private final static Random random = new Random(System.currentTimeMillis());
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
// [left..right]
int randomIndex = left + random.nextInt(right - left + 1);
swap(nums, left, randomIndex);
int pivot = nums[left];
int lt = left; // lt: less than
int gt = right + 1; // ge: greater than
// all in nums[left + 1..lt] < pivot
// all in nums(lt..i) = pivot
// all in nums[gt..right] > pivot
int i = left + 1;
while (i < gt) {
if (nums[i] < pivot) {
lt++;
swap(nums, i, lt);
i++;
} else if (nums[i] == pivot) {
i++;
} else {
// nums[i] > pivot
gt--;
swap(nums, i, gt);
}
}
swap(nums, left, lt);
quickSort(nums, left, lt - 1);
quickSort(nums, gt, right);
}
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
使用三路快排是为了避免下面这种情况:「切分」的时候有大量元素的值与
pivot的值相同。「三路快排」把与pivot相同的元素划分到了未排定部分的「中间」。
# 快速排序的优化(针对大量重复元素)
参考资料:https://www.yuque.com/liweiwei1419/algo/xu4otc
参考代码:
Java 代码:
import java.util.Random;
public class Solution {
// 快速排序 3:三指针快速排序
/**
* 列表大小等于或小于该大小,将优先于 quickSort 使用插入排序
*/
private static final int INSERTION_SORT_THRESHOLD = 7;
private static final Random RANDOM = new Random();
public int[] sortArray(int[] nums) {
int len = nums.length;
quickSort(nums, 0, len - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right) {
// 小区间使用插入排序
if (right - left <= INSERTION_SORT_THRESHOLD) {
insertionSort(nums, left, right);
return;
}
int randomIndex = left + RANDOM.nextInt(right - left + 1);
swap(nums, randomIndex, left);
// 循环不变量:
// all in [left + 1, lt] < pivot
// all in [lt + 1, i) = pivot
// all in [gt, right] > pivot
int pivot = nums[left];
int lt = left;
int gt = right + 1;
int i = left + 1;
while (i < gt) {
if (nums[i] < pivot) {
lt++;
swap(nums, i, lt);
i++;
} else if (nums[i] == pivot) {
i++;
} else {
gt--;
swap(nums, i, gt);
}
}
swap(nums, left, lt);
// 注意这里,大大减少了两侧分治的区间
quickSort(nums, left, lt - 1);
quickSort(nums, gt, right);
}
/**
* 对数组 nums 的子区间 [left, right] 使用插入排序
*
* @param nums 给定数组
* @param left 左边界,能取到
* @param right 右边界,能取到
*/
private void insertionSort(int[] nums, int left, int right) {
for (int i = left + 1; i <= right; i++) {
int temp = nums[i];
int j = i;
while (j > left && nums[j - 1] > temp) {
nums[j] = nums[j - 1];
j--;
}
nums[j] = temp;
}
}
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
Python 代码:
# 快速排序
# 三路快速排序,在有很多相等元素的情况下,最优
# 特别注意,与标定点相等的元素的处理
class QuickSortThreeWays:
def __str__(self):
return "三路快排"
def __partition(self, arr, left, right):
p = arr[left]
# 循环不变式
# (left, lt] < pivot
# [lt + 1, i) = pivot
# [gt, right] > pivot
lt = left
gt = right + 1
i = left + 1
while i < gt:
if arr[i] < p:
lt += 1
arr[i], arr[lt] = arr[lt], arr[i]
i += 1
elif arr[i] == p:
i += 1
else:
gt -= 1
arr[i], arr[gt] = arr[gt], arr[i]
arr[left], arr[lt] = arr[lt], arr[left]
return lt, gt
def __quick_sort(self, arr, left, right):
if left >= right:
return
lt, gt = self.__partition(arr, left, right)
# 在有很多重复元素的排序任务中,lt 和 gt 可能会相距很远
# 因此后序递归调用的区间变小
# 递归的深度也大大降低了
self.__quick_sort(arr, left, lt - 1)
self.__quick_sort(arr, gt, right)
def sort(self, arr):
size = len(arr)
self.__quick_sort(arr, 0, size - 1)
复杂度分析:
- 时间复杂度:
,这里 是数组的长度; - 空间复杂度:
,这里占用的空间主要来自递归函数的栈空间。
作者:liweiwei1419 链接:https://suanfa8.com/quick-sort/quick-sort-three-ways 来源:算法吧 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。