# 第 5 节双路快排

# 视频讲解

建议快进播放。

6-5 双路快排 (opens new window)

参考代码：

import java.util.Random;


class Solution {

    private final static Random random = new Random(System.currentTimeMillis());

    public int[] sortArray(int[] nums) {
        quickSort(nums, 0, nums.length - 1);
        return nums;
    }

    private void quickSort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }

        int pivotIndex = partition(nums, left, right);
        quickSort(nums, left, pivotIndex - 1);
        quickSort(nums, pivotIndex + 1, right);
    }

    private int partition(int[] nums, int left, int right) {
        // [left..right]
        int randomIndex = left + random.nextInt(right - left + 1);
        swap(nums, left, randomIndex);

        int pivot = nums[left];

        int le = left + 1; // le: less equals
        int ge = right; // ge: greater equals
        // all in nums[left + 1..le) <= pivot
        // all in nums(ge..right] >= pivot
        while (true) {
            while (le <= ge && nums[le] < pivot) {
                le++;
            }

            while (le <= ge && nums[ge] > pivot) {
                ge--;
            }

            // le 来到了第一个大于等于 pivot 的位置
            // ge 来到了第一个小于等于 pivot 的位置

            if (le >= ge) {
                break;
            }
            swap(nums, le, ge);
            le++;
            ge--;
        }

        swap(nums, left, ge);
        return ge;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }

}

针对特殊测试用例（有很多重复元素的输入数组）有 3 种版本的快排：

版本 1：基本快排：把等于切分元素的所有元素分到了数组的同一侧，可能会造成递归树倾斜；
版本 2：双指针快排：把等于切分元素的所有元素 等概率 地分到了数组的两侧，避免了递归树倾斜，递归树相对平衡；
版本 3：三指针快排：把等于切分元素的所有元素挤到了数组的中间，在有很多元素和切分元素相等的情况下，递归区间大大减少。

这里有一个经验的总结：之所以快排有这些优化，起因都是来自「递归树」的高度。关于「树」的算法的优化，绝大部分都是在和树的「高度」较劲。类似的通过减少树高度、使得树更平衡的数据结构还有「二叉搜索树」优化成「AVL 树」或者「红黑树」、「并查集」的「按秩合并」与「路径压缩」。

写对「快速排序」的技巧：保持「循环不变量」，即定义的变量在循环开始前、循环过程中、循环结束以后，都保持不变的性质，这个性质是人为根据问题特点定义的。
「循环不变量」的内容在《算法导论》这本书里有介绍。我个人觉得非常有用。「循环不变量」是证明算法有效性的基础，更是写对代码的保证，遵守循环不变量，是不是该写等于号，先交换还是先 ++ ，就会特别清楚，绝对不会写错，我在编码的时候，会将遵守的「循环不变量」作为注释写在代码中。

快速排序丢失了稳定性，如果需要稳定的快速排序，需要具体定义比较函数，这个过程叫「稳定化」，在这里就不展开了。

使用「快速排序」解决的经典问题（非常重要）：

TopK 问题：「力扣」第 215 题：数组中的第 K 个最大元素 (opens new window)；
荷兰国旗问题：「力扣」第 75 题：颜色分类 (opens new window)。

参考资料：https://www.yuque.com/liweiwei1419/algo/lopi3w

交换操作对有一种类型的数组是失效的，那就是有多个重复元素的数组。

在整个数组包含有大量重复元素的情况下，放在中间的那个 j 的位置也会使得递归的过程变得很不平衡，这个时候我们也可以采取一定的优化措施；
我们优化的思路是：使得切分元素 v 平衡地分散到 j 的两边。

参考代码：

Java 代码：

import java.util.Random;

public class Solution {

    // 快速排序 2：双指针（指针对撞）快速排序

    /**
     * 列表大小等于或小于该大小，将优先于 quickSort 使用插入排序
     */
    private static final int INSERTION_SORT_THRESHOLD = 7;

    private static final Random RANDOM = new Random();

    public int[] sortArray(int[] nums) {
        int len = nums.length;
        quickSort(nums, 0, len - 1);
        return nums;
    }

    private void quickSort(int[] nums, int left, int right) {
        // 小区间使用插入排序
        if (right - left <= INSERTION_SORT_THRESHOLD) {
            insertionSort(nums, left, right);
            return;
        }

        int pIndex = partition(nums, left, right);
        quickSort(nums, left, pIndex - 1);
        quickSort(nums, pIndex + 1, right);
    }

    /**
     * 对数组 nums 的子区间 [left, right] 使用插入排序
     *
     * @param nums  给定数组
     * @param left  左边界，能取到
     * @param right 右边界，能取到
     */
    private void insertionSort(int[] nums, int left, int right) {
        for (int i = left + 1; i <= right; i++) {
            int temp = nums[i];
            int j = i;
            while (j > left && nums[j - 1] > temp) {
                nums[j] = nums[j - 1];
                j--;
            }
            nums[j] = temp;
        }
    }

    private int partition(int[] nums, int left, int right) {
        int randomIndex = left + RANDOM.nextInt(right - left + 1);
        swap(nums, randomIndex, left);

        int pivot = nums[left];
        int lt = left + 1;
        int gt = right;

        // 循环不变量：
        // all in [left + 1, lt) <= pivot
        // all in (gt, right] >= pivot
        while (true) {
            while (lt <= right && nums[lt] < pivot) {
                lt++;
            }

            while (gt > left && nums[gt] > pivot) {
                gt--;
            }

            if (lt > gt) {
                break;
            }

            // 细节：相等的元素通过交换，等概率分到数组的两边
            swap(nums, lt, gt);
            lt++;
            gt--;
        }
        swap(nums, left, gt);
        return gt;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }
}

Python 代码：

# 快速排序
# 在 partition 的过程中使用指针对撞的
# 特别注意，与标定点相等的元素的处理

# 双路快排：
# 随机将与标定点相等的元素分配到左边和右边
# 针对有许多重复键值的数组进行排序
class QuickSortTwoWays:

    def __str__(self):
        return "双路快排"

    def __partition(self, arr, left, right):
        p = arr[left]
        le = left + 1
        ge = right
        while True:
            # 针对索引进行判断的时候，要考虑是否越界
            while le <= right and arr[le] < p:
                le += 1
            while ge >= left + 1 and arr[ge] > p:
                ge -= 1
            if le > ge:
                break
            arr[le], arr[ge] = arr[ge], arr[le]
            le += 1
            ge -= 1
        # 注意：这里交换 left 与 ge 的位置
        arr[left], arr[ge] = arr[ge], arr[left]
        return ge

    def __quick_sort(self, arr, left, right):
        if left >= right:
            return
        p_index = self.__partition(arr, left, right)
        self.__quick_sort(arr, left, p_index - 1)
        self.__quick_sort(arr, p_index + 1, right)

    def sort(self, arr):
        size = len(arr)
        self.__quick_sort(arr, 0, size - 1)

# 解释最后为什么交换 `left` 与 `ge`

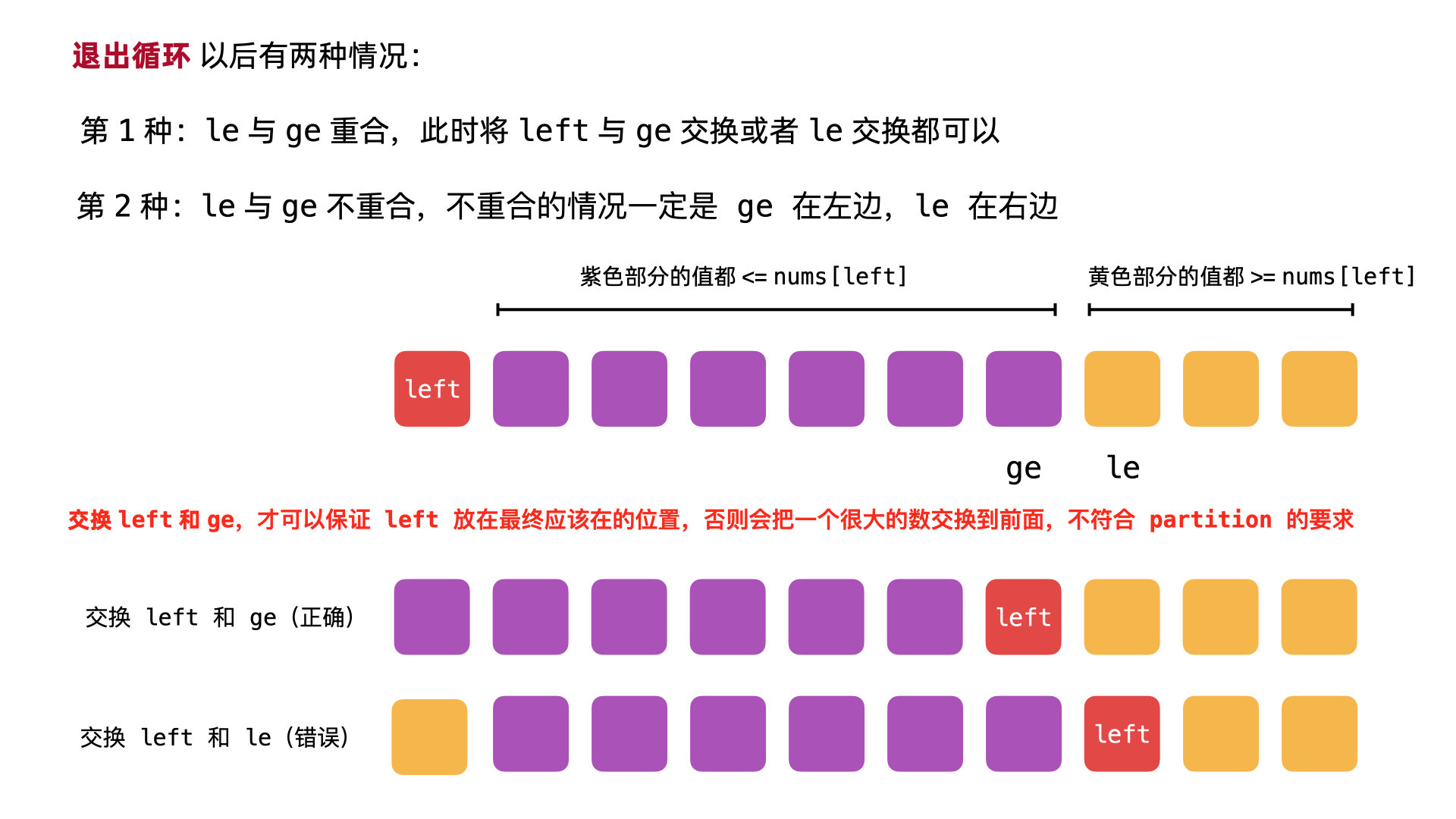
作者：liweiwei1419 链接：https://suanfa8.com/quick-sort/quick-sort 来源：算法吧著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

← 第 4 节随机选择切分元素第 6 节三路快排 →

# 第 5 节 双路快排

# 视频讲解

# 解释最后为什么交换 left 与 ge

# 第 5 节双路快排

# 解释最后为什么交换 `left` 与 `ge`