# 基数排序
说明:本节内容不重要,不用仔细看。
基本思路:也称为基于关键字的排序,例如针对数值排序,个位、十位、百位就是关键字。针对日期数据的排序:年、月、日、时、分、秒就是关键字。
「基数排序」用到了「计数排序」。
摘要:基数排序是一种基于「关键字」的排序方法,这里的「关键字」是每一个数位,重点在于理解结论:低位优先的有效性。
重点理解:基数排序的子过程:计数排序(因为要保证稳定性)。
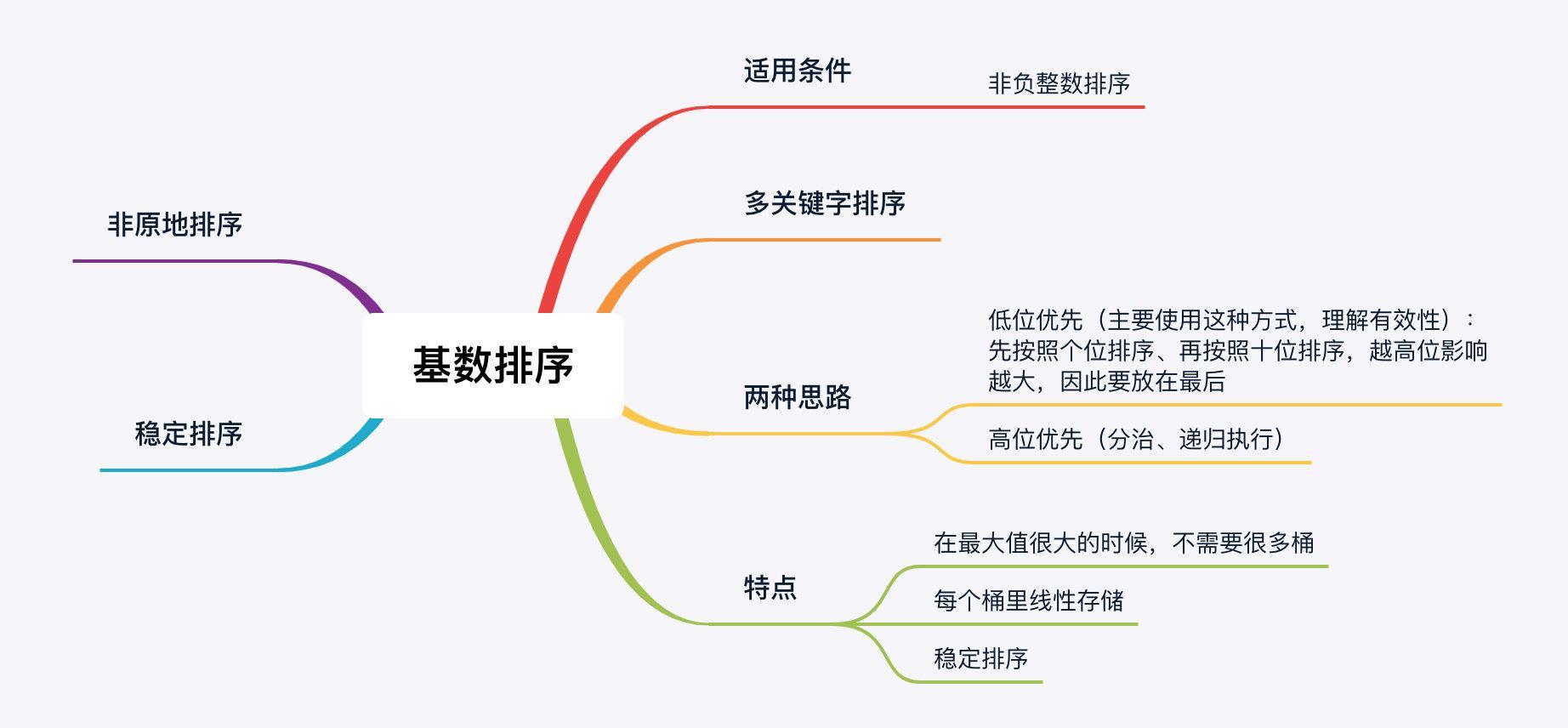
# 基数排序简介
- 基数排序是一种非比较的排序方法,它是多关键字的排序方法;
- 为了使得基数排序的描述更为直观,我们只以非负整数的排序任务为例;
- 在基数排序中认为一个整数的个位、十位分别是一个关键字。
基数排序有两种方式:高位优先(Most significant digital)和低位优先(Least significant digital)。常见的做法是 低位优先,对高位优先我们只做简单介绍,重点介绍低位优先。
# 高位优先(不推荐)
# 基数排序(高位优先)的基本思路
高位优先比较直观:先按照高位升序排序,然后按照次高位排序,依次这样进行下去排到最低位。

该方法的实现使用了「分而治之」的思想递归执行下去,需要借助递归方法实现,且空间复杂度较大。事实上,完全可以先按照低位排序,一直排到最高位。这种做法不仅仅是正确的,实现起来还更简单。
# 低位优先(推荐)
我们通过一个具体的例子,看一下低位优先是如何排序的。例如:[329, 457, 657, 839, 436, 720, 355],使用基数排序的「低位优先」算法执行流程。
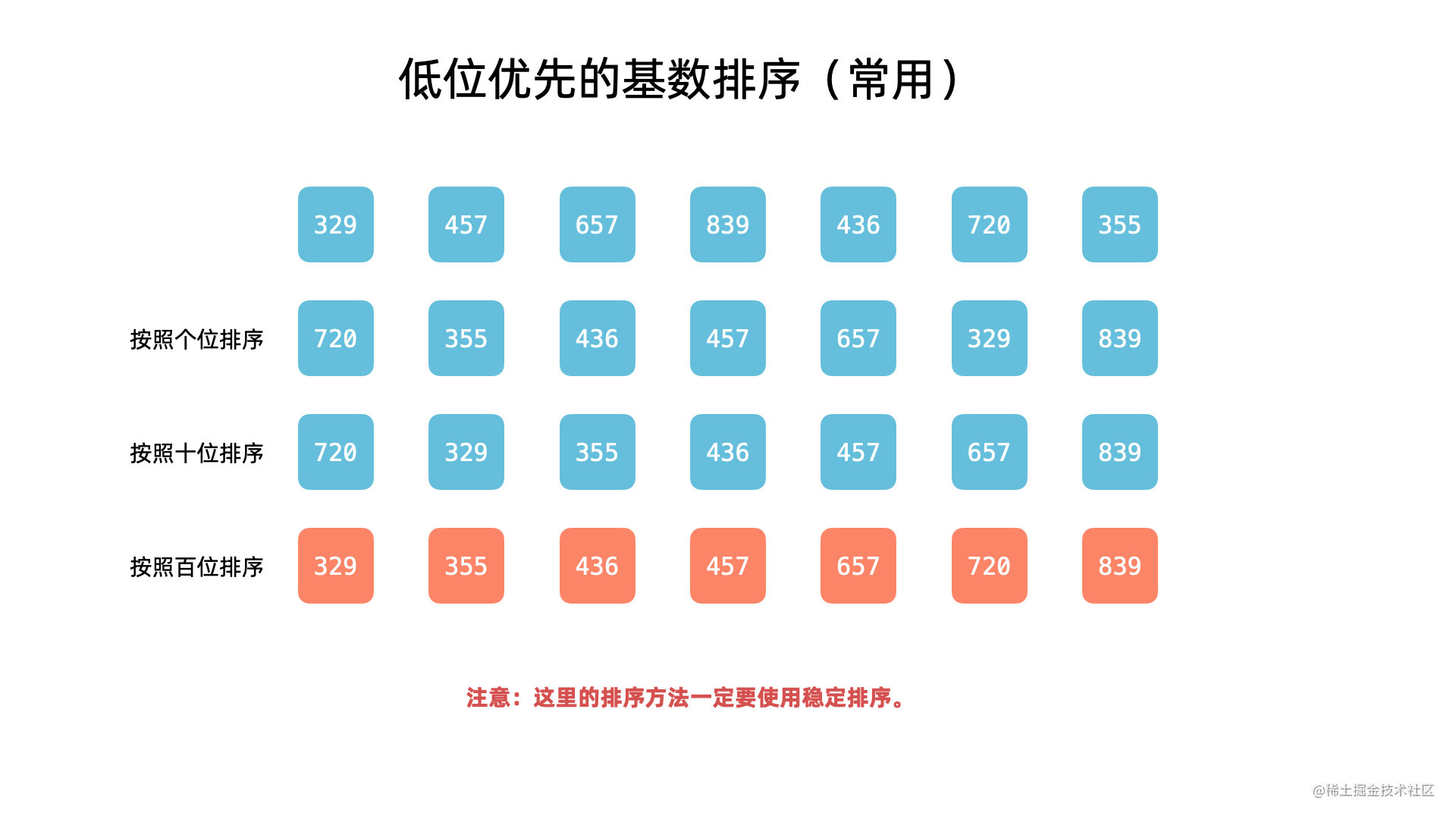
- 首先按照个位数字进行一次 稳定排序(相同数字顺序不变),得到
[720, 355, 436, 457, 657, 329, 839]; - 然后按照十位数字进行一次 稳定排序(相同数字顺序不变),得到
[720, 329, 436, 839, 355, 457, 657]; - 然后按照百位数字进行一次 稳定排序(相同数字顺序不变),得到
[329, 355, 436, 457, 657, 720, 839]。
# 低位优先的有效性
我们比较两个数字的时候,总是先比较最高位。低位优先的基数排序,越高位的排序是放在后面进行的,在高位相同的情况下,需要比较次高位,而次高位在之前的排序中已经排好序。
这其中非常重要的一点是,每一趟基于关键字的排序 必须使用稳定排序,请大家在理解了上面的例子以后仔细体会这一点。
# 代码编写
细节:如何得到每个数位上的数值。
- 先把低位抹去;
- 再取个位(模
即可)。
// 计算数位上的数是几,先取个位,再十位、百位
int remainder = (arr[j] / divisor) % 10;
完整代码:「力扣」第 912 题
Java 代码:
public class RadixSort {
public void sort(int[] nums) {
int len = nums.length;
// 第 1 步:找出最大的数字
int max = nums[0];
for (int i = 0; i < len; i++) {
if (nums[i] > max) {
max = nums[i];
}
// 数据有效性校验,因为要将数值作为 count 的索引用,因此 nums[i] 不能小于 0
if (nums[i] < 0) {
throw new IllegalArgumentException("该数组不适合使用计数排序");
}
}
// 第 2 步:计算出最大的数字有几位,这个数值决定了我们要将整个数组看几遍
int maxLen = getMaxLen(max);
// 第 3 步:每一趟都使用计数排序
int[] count = new int[10];
int[] temp = new int[len];
int divisor = 1;
// 有几位数,外层循环就得执行几次
for (int i = 0; i < maxLen; i++) {
// 每一步都使用计数排序,保证排序结果是稳定的,这一步需要额外空间保存结果集,因此把结果保存在 temp 中
countingSort(nums, temp, divisor, len, count);
System.arraycopy(temp, 0, nums, 0, len);
divisor *= 10;
}
}
/**
*
* @param nums 原始数组
* @param temp 在计数排序的过程中使用的辅助数组,这一次基于 divisor 关键字的排序结果存在这里
* @param divisor
* @param len 原始数组的长度(冗余变量)
* @param count 计数数组
*/
private void countingSort(int[] nums, int[] temp, int divisor, int len, int[] count) {
// 内层循环得把数组从头到尾看一遍
for (int j = 0; j < len; j++) {
// 计算数位上的数是几,先取个位,再十位、百位
int remainder = (nums[j] / divisor) % 10;
count[remainder]++;
}
for (int j = 1; j < 10; j++) {
count[j] += count[j - 1];
}
for (int j = len - 1; j >= 0; j--) {
int remainder = (nums[j] / divisor) % 10;
int index = count[remainder] - 1;
temp[index] = nums[j];
count[remainder]--;
}
// 重置数组 count,以便下次使用
for (int j = 0; j < 10; j++) {
count[j] = 0;
}
}
/**
* 获取一个整数的最大位数
*
* @param num
* @return
*/
private int getMaxLen(int num) {
int maxLen = 0;
while (num > 0) {
num /= 10;
maxLen++;
}
return maxLen;
}
}
Java 代码:
public class Solution {
// 基数排序:低位优先
private static final int OFFSET = 50000;
public int[] sortArray(int[] nums) {
int len = nums.length;
// 预处理,让所有的数都大于等于 0,这样才可以使用基数排序
for (int i = 0; i < len; i++) {
nums[i] += OFFSET;
}
// 第 1 步:找出最大的数字
int max = nums[0];
for (int num : nums) {
if (num > max) {
max = num;
}
}
// 第 2 步:计算出最大的数字有几位,这个数值决定了我们要将整个数组看几遍
int maxLen = getMaxLen(max);
// 计数排序需要使用的计数数组和临时数组
int[] count = new int[10];
int[] temp = new int[len];
// 表征关键字的量:除数
// 1 表示按照个位关键字排序
// 10 表示按照十位关键字排序
// 100 表示按照百位关键字排序
// 1000 表示按照千位关键字排序
int divisor = 1;
// 有几位数,外层循环就得执行几次
for (int i = 0; i < maxLen; i++) {
// 每一步都使用计数排序,保证排序结果是稳定的
// 这一步需要额外空间保存结果集,因此把结果保存在 temp 中
countingSort(nums, temp, divisor, len, count);
// 交换 nums 和 temp 的引用,下一轮还是按照 nums 做计数排序
int[] t = nums;
nums = temp;
temp = t;
// divisor 自增,表示采用低位优先的基数排序
divisor *= 10;
}
int[] res = new int[len];
for (int i = 0; i < len; i++) {
res[i] = nums[i] - OFFSET;
}
return res;
}
private void countingSort(int[] nums, int[] res, int divisor, int len, int[] count) {
// 1、计算计数数组
for (int i = 0; i < len; i++) {
// 计算数位上的数是几,先取个位,再十位、百位
int remainder = (nums[i] / divisor) % 10;
count[remainder]++;
}
// 2、变成前缀和数组
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 3、从后向前赋值
for (int i = len - 1; i >= 0; i--) {
int remainder = (nums[i] / divisor) % 10;
int index = count[remainder] - 1;
res[index] = nums[i];
count[remainder]--;
}
// 4、count 数组需要设置为 0 ,以免干扰下一次排序使用
for (int i = 0; i < 10; i++) {
count[i] = 0;
}
}
/**
* 获取一个整数的最大位数
*
* @param num
* @return
*/
private int getMaxLen(int num) {
int maxLen = 0;
while (num > 0) {
num /= 10;
maxLen++;
}
return maxLen;
}
}
复杂度分析:(这部分内容不太重要,增加学习负担)
- 时间复杂度:
,这里 为输入数组的长度, 为关键字的个数。以非负整数数组的排序任务为例,最大值有几位( )就需要看数组几遍; - 空间复杂度:
,这里 (一个数的位数)通常比 (输入数组的长度)小很多。
# 总结
基数排序是稳定排序(要求子过程也必须是稳定排序),且是非原地进行的。我们继续完善表格:
| 最坏时间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 额外空间复杂度 | 稳定性 | 是否原地排序 | |
|---|---|---|---|---|---|---|
| 选择排序 | 不稳定 | 原地排序 | ||||
| 冒泡排序 | 稳定 | 原地排序 | ||||
| 插入排序 | 稳定 | 原地排序 | ||||
| 希尔排序 | (没有相关研究) | 不稳定 | 原地排序 | |||
| 归并排序 | 稳定 | 非原地排序 | ||||
| 快速排序 | 不稳定 | 原地排序 | ||||
| 计数排序 | 稳定 | 非原地排序 | ||||
| 基数排序 | 稳定 | 非原地排序 |
说明:
- 计数排序中,
是数组的长度, 是数组的最大值(假设数组的最小值为 ); - 基数排序中,
是数组的长度, 是最大值的位数(关键字的个数)。
# 练习
- 使用基数数排序完成「力扣」第 912 题:排序数组(中等)。
说明:注意题目中给出的输入数组元素的数值范围。
这一节重点在于理解「基数排序」是一种基于多关键字的排序方法,并且通过具体的例子理解「低位优先」的合理性是由每一位数上的 稳定排序 保证的。
本节内容已经发布在 掘金博客 (opens new window)。
作者:liweiwei1419 链接:https://suanfa8.com/non-comparison-sorting-algorithm/radix-sort 来源:算法吧 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
← 第 1 节 计数排序 第 3 节 桶排序 →