第 4 节 随机选择切分元素

• 问题：对于顺序数组或者逆序数组来说，递归树高度增加、递归树倾斜；
• 再提出解决方案：破坏顺序性，随机选择 pivot。

参考代码：

import java.util.Random;


class Solution {

    private final static Random random = new Random(System.currentTimeMillis());

    public int[] sortArray(int[] nums) {
        quickSort(nums, 0, nums.length - 1);
        return nums;
    }

    private void quickSort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }

        int pivotIndex = partition(nums, left, right);
        quickSort(nums, left, pivotIndex - 1);
        quickSort(nums, pivotIndex + 1, right);
    }

    private int partition(int[] nums, int left, int right) {
        // [left..right]
        int randomIndex = left + random.nextInt(right - left + 1);
        swap(nums, left, randomIndex);

        int pivot = nums[left];

        int j = left + 1;
        // all in nums[left + 1..j) <= pivot
        // all in nums[j..i) > pivot
        for (int i = left + 1; i <= right; i++){
            if (nums[i] <= pivot) {
                swap(nums, i, j);
                j++;
            }
        }
        swap(nums, left, j - 1);
        return j - 1;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }

}

---

快速排序对于有序的数组并没有那么友好，下面我们具体来分析是一下是怎么回事。

避免这种最坏的情况出现，我们在切分 partition 之前，只需要在待排序的区间里，随机选择一个元素交换到数组的第 1 个位置就可以了，这样，最坏的情况出现的概率就极其低了。

针对特殊测试用例（顺序数组或者逆序数组）一定要随机化选择切分元素（pivot），否则在输入数组是有序数组或者是逆序数组的时候，快速排序会变得非常慢（等同于冒泡排序或者「选择排序」）。

优化 1：随机选择标定点元素，降低递归树结构不平衡的情况

由于快速排序在近乎有序的时候会非常差，此时递归树的深度会增加。此时快速排序的算法就退化为 。

解决办法：我们在每一次迭代开始之前，随机选取一个元素作为基准元素与第 1 个元素交换即可。

int randomIndex = random.nextInt(right - left + 1) + left;
swap(arr,left,randomIndex);
int v = arr[left];

优化 2：小区间使用插入排序

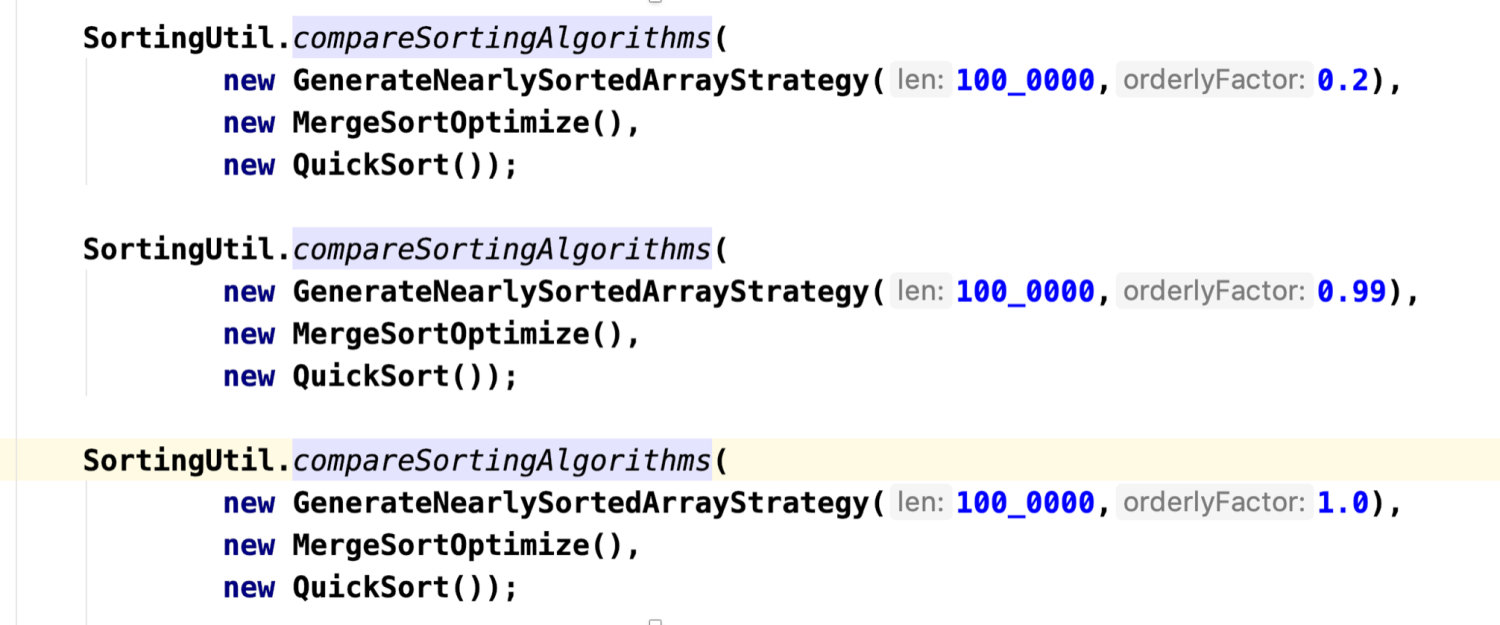
• 在第 1 版快速排序的实现上，结合我们对第 1 版归并排序的讨论，我们可以知道：在待排序区间长度比较短的时候可以使用插入排序来提升排序效率，同样，我们使用 作为临界值；
• 测试用例：近乎有序的数组，100 万，归并排序，快速排序。

参考代码：

说明：

• lt 是 less than 的缩写，表示（严格）小于；
• gt 是 greater than 的缩写，表示（严格）大于；
• le 是 less than or equal 的缩写，表示小于等于（本代码没有用到）；
• ge 是 greater than or equal 的缩写，表示大于等于（本代码没有用到）。

Java 代码：

import java.util.Random;

public class Solution {

    // 快速排序 1：基本快速排序

    /**
     * 列表大小等于或小于该大小，将优先于 quickSort 使用插入排序
     */
    private static final int INSERTION_SORT_THRESHOLD = 7;

    private static final Random RANDOM = new Random();


    public int[] sortArray(int[] nums) {
        int len = nums.length;
        quickSort(nums, 0, len - 1);
        return nums;
    }

    private void quickSort(int[] nums, int left, int right) {
        // 小区间使用插入排序
        if (right - left <= INSERTION_SORT_THRESHOLD) {
            insertionSort(nums, left, right);
            return;
        }

        int pIndex = partition(nums, left, right);
        quickSort(nums, left, pIndex - 1);
        quickSort(nums, pIndex + 1, right);
    }

    /**
     * 对数组 nums 的子区间 [left, right] 使用插入排序
     *
     * @param nums  给定数组
     * @param left  左边界，能取到
     * @param right 右边界，能取到
     */
    private void insertionSort(int[] nums, int left, int right) {
        for (int i = left + 1; i <= right; i++) {
            int temp = nums[i];
            int j = i;
            while (j > left && nums[j - 1] > temp) {
                nums[j] = nums[j - 1];
                j--;
            }
            nums[j] = temp;
        }
    }

    private int partition(int[] nums, int left, int right) {
        int randomIndex = RANDOM.nextInt(right - left + 1) + left;
        swap(nums, left, randomIndex);

        // 基准值
        int pivot = nums[left];
        int lt = left;
        // 循环不变量：
        // all in [left + 1, lt] < pivot
        // all in [lt + 1, i) >= pivot
        for (int i = left + 1; i <= right; i++) {
            if (nums[i] < pivot) {
                lt++;
                swap(nums, i, lt);
            }
        }
        swap(nums, left, lt);
        return lt;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }
}

Python 代码：

from sorting.sorting_util import SortingUtil


class QuickSort:

    def __str__(self):
        return "最基本的快速排序"

    def __partition(self, arr, left, right):
        """对区间 [left, right] （包括左右端点）执行 partition 操作，将 pivot 挪到它最终应该在的位置"""
        pivot = arr[left]
        lt = left
        # 循环不变式
        # [left, lt - 1] < pivot，初始时，lt - 1 = left - 1
        # [lt, i) >= pivot，初始时，[left, left + 1)
        # i 的性质在循环开始的时候，不能推测出，我们就是要在循环中保持这个性质
        for i in range(left + 1, right + 1):
            if arr[i] < pivot:
                lt += 1
                arr[lt], arr[i] = arr[i], arr[lt]

        arr[left], arr[lt] = arr[lt], arr[left]
        return lt

    def __quick_sort(self, nums, left, right):
        """在区间 [left, right] （包括左右端点）执行快速排序操作"""
        if left >= right:
            return
        p_index = self.__partition(nums, left, right)
        self.__quick_sort(nums, left, p_index - 1)
        self.__quick_sort(nums, p_index + 1, right)

    def sort(self, arr):
        size = len(arr)
        self.__quick_sort(arr, 0, size - 1)

下面我们测试一下刚刚写好的快速排序的代码。测试要点：

1. 测试正确性；
2. 与归并排序比较；快速排序已经快了一些。

---

作者：liweiwei1419 链接：https://suanfa8.com/quick-sort/random-select-pivot 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。