第 5 版 quick-union 基于路径压缩的非递归实现

重点概括：这一版代码用得最多。因为好理解，且代码量较少。

只用理解这一句即可 parent[p] = parent[parent[p]];，可以称之为「隔代压缩」。

虽然压缩不彻底，但是多压缩几次也就能够达到完全压缩的效果，且不使用递归，不占用「递归栈」空间。

路径压缩 path Compression

什么是路径压缩 path Compression？以上我们都是针对于 union 操作的优化，其实我们在 find 的时候，就可以对一棵树进行整理，让它的高度变低，这一点是基于并查集的一个特性：只要它们是连在一起的，其实谁指向谁，并不重要，所以我们在接下来的讨论中看到的并查集的表示图，它们是等价的，即它们表示的都是同一个并查集。

路径压缩 path Compression 的思路：在 find 的时候一次又一次的整理，将并查集构造（整理）成一个与之等价的并查集，使得后续的每一次 find 这样的操作路径最短。

假设一个最极端的并查集的图表示如下：

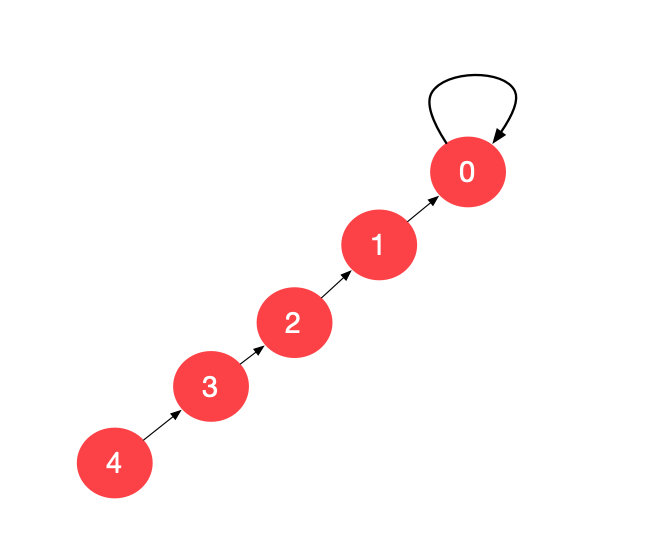
我们开始找 的父亲结点， 的父亲结点不是 ，说明不是根结点，此时，我们尝试 步一跳，将 的父亲结点改成 的父亲结点的父亲结点，于是得到一个等价的并查集：

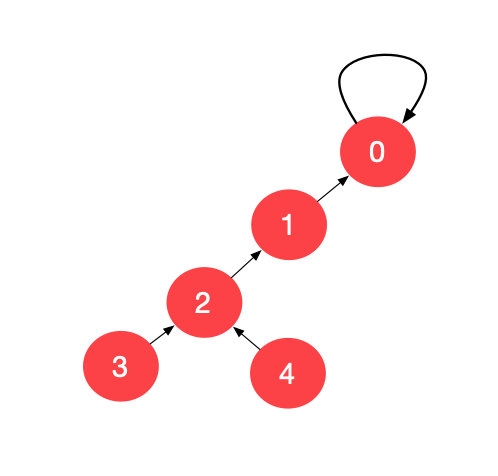
下面我们该考察元素 了， 的父亲结点是 ， 不是根结点，所以我们继续两步一跳，把 的父亲结点设置成它的父亲结点的父亲结点，于是又得到一个等价的并查集：

此时，整棵树的高度就在一次 find 的过程中被压缩了。这里有一个疑问：即使我们在最后只差一步的情况下，我们跳两步，也不会出现无效的索引。其实，一步一跳，两步一跳，甚至三步一跳都没有关系。

画图画了这么多，代码实现只有一行：parent[p] = parent[parent[p]]; 编写的时候要注意这行代码添加的位置，画一个示意图，想想这个路径压缩的过程，就不难写出。

Java 代码：

public int find(int p) {
    // 在 find 的时候执行路径压缩
    while (p != parent[p]) {
        // 编写这句代码的时候可能会觉得有点绕，
        // 画一个示意图，就能很直观地写出正确的逻辑
        // 两步一跳完成路径压缩
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

根据上面的图，我们通过 find 操作执行路径压缩，最终形成的并查集如下：

---

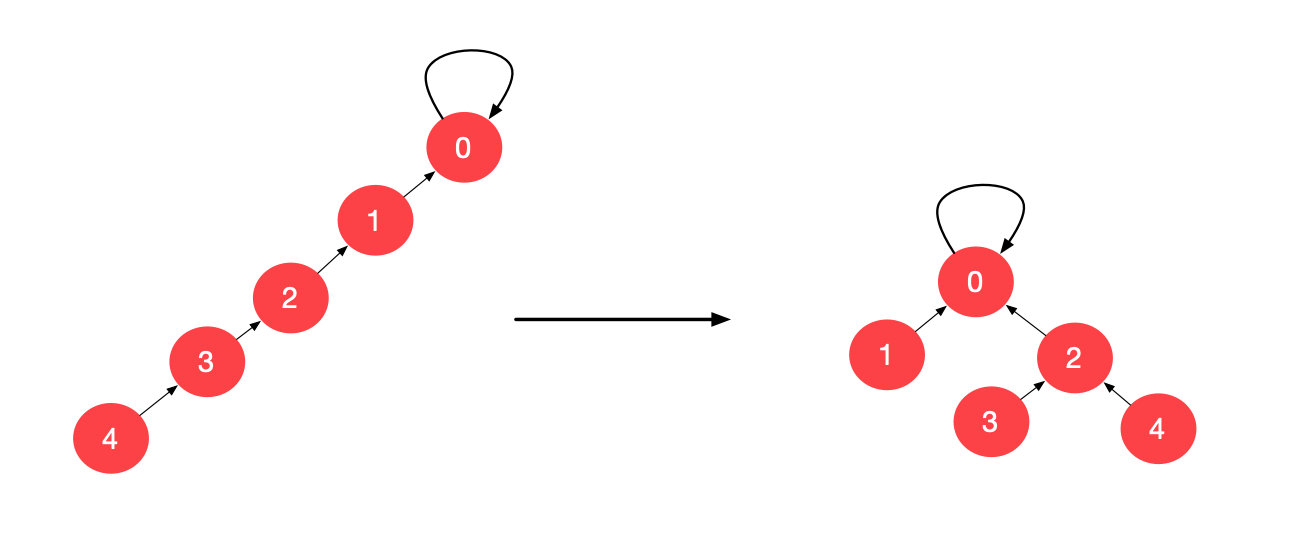
作者：liweiwei1419 链接：https://suanfa8.com/union-find/quick-union-path-compression-non-recursive 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。