第 4 版 quick-union 基于 rank 的优化

重点提示：基于 rank 的优化是使用得更多的，因为这样做更合理一些，但是维护数组 rank 的定义是相对麻烦的，通常的做法就是不维护，只是把数组 rank 作为两个集合合并的参考，即使是错的，也比随机合并的结果好。

使用 size 来决定将哪个结点的根指向另一个结点的根，其实并不太合理，但并不能说不正确，因为谁的根指向谁的根，其实都没有错，下面就是一个特殊的情况。

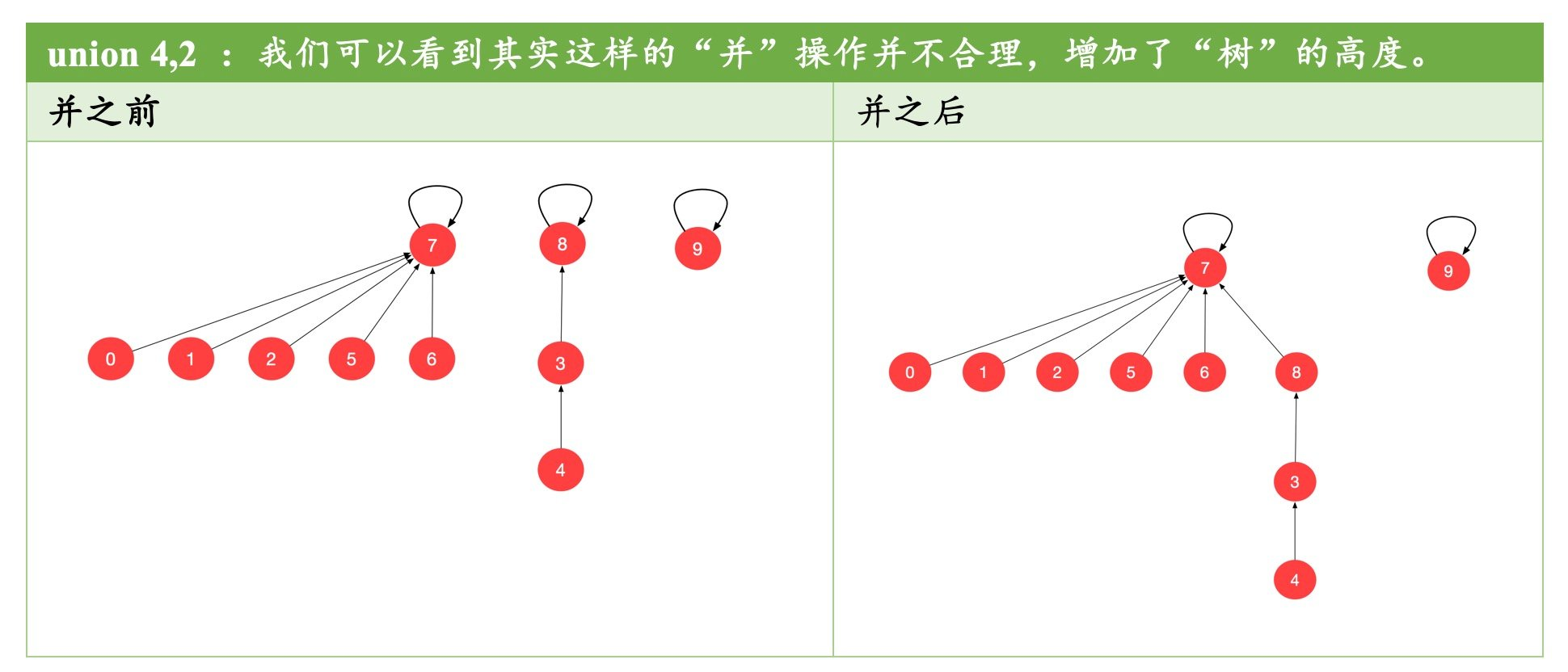
因为我们总是期望这棵树的高度比较低，在这种情况下，我们在 find 的时候，就能通过很少的步数来找到根结点，进而提高 find 的效率。为此，我们引入 rank 数组，其定义是： rank[i] 表示以第 i 个元素为根的树的高度。

Java 代码：

public class UnionFind4 implements IUnionFind {

    private int[] parent;

    private int count;

    // 以下标为 i 的元素为根结点的树的深度（最深的那个深度）
    private int[] rank;

    public UnionFind4(int n) {
        this.count = n;
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            // 初始化时，所有的元素只包含它自己，只有一个元素，所以 rank[i] = 1
            rank[i] = 1;
        }
    }

    @Override
    public String versionName() {
        return "并查集的第 4 个版本，基于 parent 数组，quick-union，基于 rank";
    }

    // 返回下标为 p 的元素的根结点
    @Override
    public int find(int p) {
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public boolean isConnected(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        return pRoot == qRoot;
    }


    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 这一步是与第 3 版不同的地方
        if (rank[pRoot] > rank[qRoot]) {
            parent[qRoot] = pRoot;
        } else if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else {
            parent[qRoot] = pRoot;
            rank[pRoot]++;
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

---

作者：liweiwei1419 链接：https://suanfa8.com/union-find/quick-union-optimization-rank 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。