# 「力扣」第 22 题：括号生成（中等）

题目链接：22. 括号生成 (opens new window)；
题解链接：回溯算法（深度优先遍历）+ 广度优先遍历（Java） (opens new window)。

# 题目描述

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

1 <= n <= 8

# 思路分析

这一类问题是在一棵隐式的树上求解，可以用深度优先遍历，也可以用广度优先遍历。一般用深度优先遍历。原因是：

代码好写，使用递归的方法，直接借助系统栈完成状态的转移；
广度优先遍历得自己编写结点类和借助队列。

这里的「状态」是指程序执行到 隐式树 的某个结点的语言描述，在程序中用不同的变量加以区分。

# 方法一：深度优先遍历

我们以 n = 2 为例，画树形结构图。方法是「做减法」。

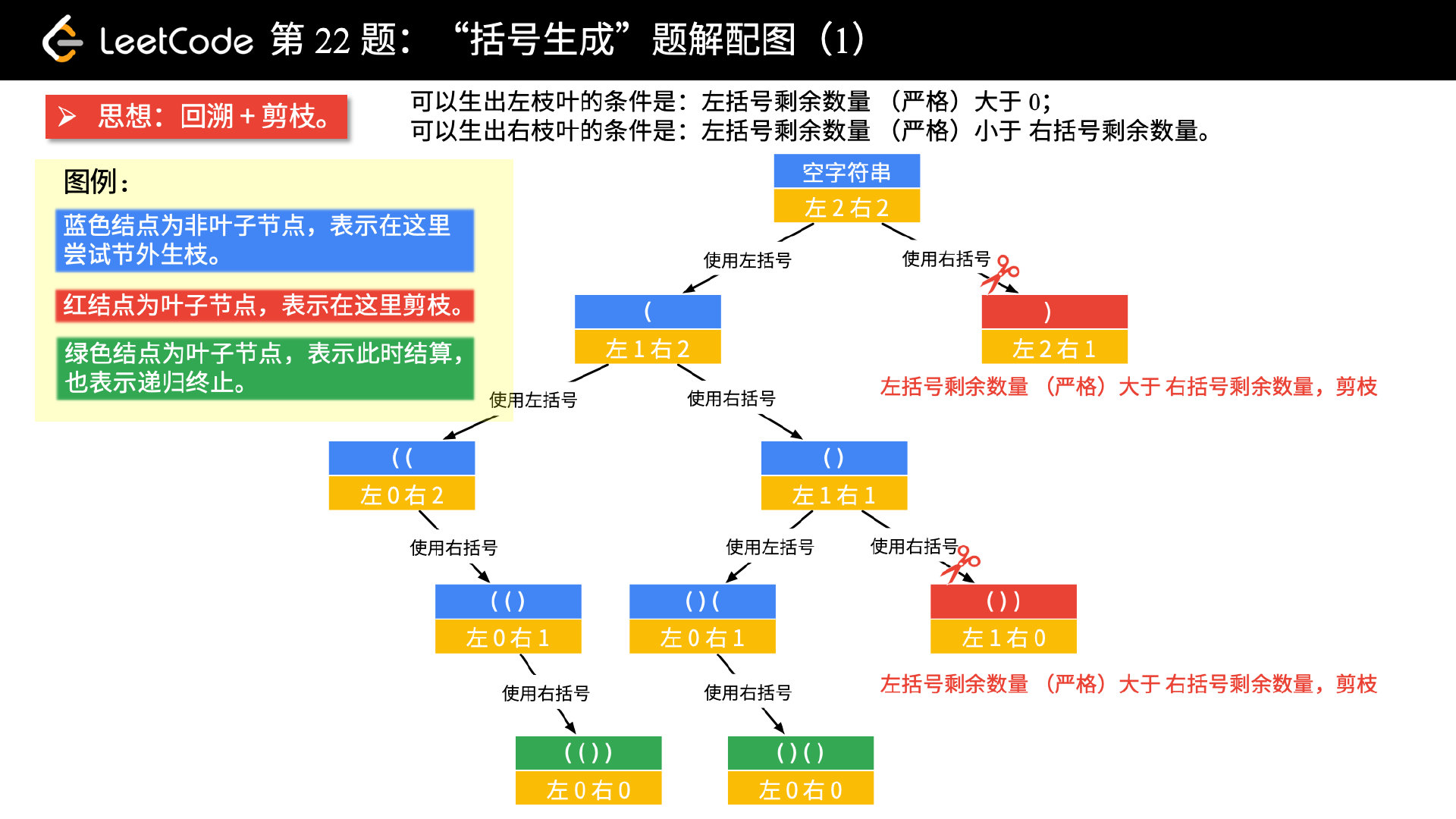
画图以后，可以分析出的结论：

当前左右括号都有大于个可以使用的时候，才产生分支；
产生左分支的时候，只看当前是否还有左括号可以使用；
产生右分支的时候，还受到左分支的限制，右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候，才可以产生分支；
在左边和右边剩余的括号数都等于的时候结算。

参考代码 1：

import java.util.ArrayList;
import java.util.List;

public class Solution {

    // 做减法

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        // 特判
        if (n == 0) {
            return res;
        }

        // 执行深度优先遍历，搜索可能的结果
        dfs("", n, n, res);
        return res;
    }

    /**
     * @param curStr 当前递归得到的结果
     * @param left   左括号还有几个可以使用
     * @param right  右括号还有几个可以使用
     * @param res    结果集
     */
    private void dfs(String curStr, int left, int right, List<String> res) {
        // 因为每一次尝试，都使用新的字符串变量，所以无需回溯
        // 在递归终止的时候，直接把它添加到结果集即可，注意与「力扣」第 46 题、第 39 题区分
        if (left == 0 && right == 0) {
            res.add(curStr);
            return;
        }

        // 剪枝（如图，左括号可以使用的个数严格大于右括号可以使用的个数，才剪枝，注意这个细节）
        if (left > right) {
            return;
        }

        if (left > 0) {
            dfs(curStr + "(", left - 1, right, res);
        }

        if (right > 0) {
            dfs(curStr + ")", left, right - 1, res);
        }
    }
}

from typing import List


class Solution:
    def generateParenthesis(self, n: int) -> List[str]:

        res = []
        cur_str = ''

        def dfs(cur_str, left, right):
            """
            :param cur_str: 从根结点到叶子结点的路径字符串
            :param left: 左括号还可以使用的个数
            :param right: 右括号还可以使用的个数
            :return:
            """
            if left == 0 and right == 0:
                res.append(cur_str)
                return
            if right < left:
                return
            if left > 0:
                dfs(cur_str + '(', left - 1, right)
            if right > 0:
                dfs(cur_str + ')', left, right - 1)

        dfs(cur_str, n, n)
        return res

我们运行 n = 2 的情况，得到结果 [(()), ()()] ，说明分析的结果是正确的。

如果我们不用减法，使用加法，即 left 表示「左括号使用了几个」，right 表示「右括号使用了几个」，可以画出另一棵递归树。

下面是参考代码。

参考代码 2：

import java.util.ArrayList;
import java.util.List;

public class Solution {

    // 做加法

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        // 特判
        if (n == 0) {
            return res;
        }

        dfs("", 0, 0, n, res);
        return res;
    }

    /**
     * @param curStr 当前递归得到的结果
     * @param left   左括号已经用了几个
     * @param right  右括号已经用了几个
     * @param n      左括号、右括号一共得用几个
     * @param res    结果集
     */
    private void dfs(String curStr, int left, int right, int n, List<String> res) {
        if (left == n && right == n) {
            res.add(curStr);
            return;
        }

        // 剪枝
        if (left < right) {
            return;
        }

        if (left < n) {
            dfs(curStr + "(", left + 1, right, n, res);
        }
        if (right < n) {
            dfs(curStr + ")", left, right + 1, n, res);
        }
    }
}

from typing import List


class Solution:
    def generateParenthesis(self, n: int) -> List[str]:

        res = []
        cur_str = ''

        def dfs(cur_str, left, right, n):
            """
            :param cur_str: 从根结点到叶子结点的路径字符串
            :param left: 左括号已经使用的个数
            :param right: 右括号已经使用的个数
            :return:
            """
            if left == n and right == n:
                res.append(cur_str)
                return
            if left < right:
                return

            if left < n:
                dfs(cur_str + '(', left + 1, right, n)

            if right < n:
                dfs(cur_str + ')', left, right + 1, n)

        dfs(cur_str, 0, 0, n)
        return res

# 方法二：广度优先遍历

通过编写广度优先遍历的代码，读者可以体会一下，为什么搜索几乎都是用深度优先遍历（回溯算法）。

广度优先遍历，得程序员自己编写结点类，显示使用队列这个数据结构。深度优先遍历的时候，就可以直接使用系统栈，在递归方法执行完成的时候，系统栈顶就把我们所需要的状态信息直接弹出，而无须编写结点类和显示使用栈。

下面的代码，读者可以把 Queue 换成 Stack，提交以后，也可以得到 Accept。

读者可以通过比较：

广度优先遍历；
自己使用栈编写深度优先遍历；
使用系统栈的深度优先遍历（回溯算法）。

来理解「回溯算法」作为一种「搜索算法」的合理性。

还是上面的题解配图（1），使用广度优先遍历，结果集都在最后一层，即叶子结点处得到所有的结果集，编写代码如下。

感谢 @liu-ren-you 朋友帮我优化了代码。

参考代码 3：（前 2 个 Java 代码写法没有本质不同，仅供参考。第 3 个 Java 代码仅仅是把 Queue 换成了 Stack ，广度优先遍历就改成了深度优先遍历。）

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class Solution {

    class Node {
        /**
         * 当前得到的字符串
         */
        private String res;
        /**
         * 剩余左括号数量
         */
        private int left;
        /**
         * 剩余右括号数量
         */
        private int right;

        public Node(String str, int left, int right) {
            this.res = str;
            this.left = left;
            this.right = right;
        }
    }

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        if (n == 0) {
            return res;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.offer(new Node("", n, n));

        while (!queue.isEmpty()) {

            Node curNode = queue.poll();
            if (curNode.left == 0 && curNode.right == 0) {
                res.add(curNode.res);
            }
            if (curNode.left > 0) {
                queue.offer(new Node(curNode.res + "(", curNode.left - 1, curNode.right));
            }
            if (curNode.right > 0 && curNode.left < curNode.right) {
                queue.offer(new Node(curNode.res + ")", curNode.left, curNode.right - 1));
            }
        }
        return res;
    }
}

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class Solution {

    class Node {
        /**
         * 当前得到的字符串
         */
        private String res;
        /**
         * 剩余左括号数量
         */
        private int left;
        /**
         * 剩余右括号数量
         */
        private int right;

        public Node(String res, int left, int right) {
            this.res = res;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "Node{" +
                    "res='" + res + '\'' +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        if (n == 0) {
            return res;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.offer(new Node("", n, n));
        // 总共需要拼凑的字符总数是 2 * n
        n = 2 * n;
        while (n > 0) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node curNode = queue.poll();
                if (curNode.left > 0) {
                    queue.offer(new Node(curNode.res + "(", curNode.left - 1, curNode.right));
                }
                if (curNode.right > 0 && curNode.left < curNode.right) {
                    queue.offer(new Node(curNode.res + ")", curNode.left, curNode.right - 1));
                }
            }
            n--;
        }

        // 最后一层就是题目要求的结果集
        while (!queue.isEmpty()) {
            res.add(queue.poll().res);
        }
        return res;
    }
}

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;

public class Solution {

    class Node {
        /**
         * 当前得到的字符串
         */
        private String res;
        /**
         * 剩余左括号数量
         */
        private int left;
        /**
         * 剩余右括号数量
         */
        private int right;

        public Node(String str, int left, int right) {
            this.res = str;
            this.left = left;
            this.right = right;
        }
    }

    // 注意：这是深度优先遍历

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        if (n == 0) {
            return res;
        }

        // 查看了 Stack 源码，官方推荐使用 Deque 对象，
        // 注意：只使用栈相关的接口，即只使用 `addLast()` 和 `removeLast()`
        Deque<Node> stack = new ArrayDeque<>();
        stack.addLast(new Node("", n, n));

        while (!stack.isEmpty()) {

            Node curNode = stack.removeLast();
            if (curNode.left == 0 && curNode.right == 0) {
                res.add(curNode.res);
            }
            if (curNode.left > 0) {
                stack.addLast(new Node(curNode.res + "(", curNode.left - 1, curNode.right));
            }
            if (curNode.right > 0 && curNode.left < curNode.right) {
                stack.addLast(new Node(curNode.res + ")", curNode.left, curNode.right - 1));
            }
        }
        return res;
    }
}

作者：liweiwei1419 链接：https://suanfa8.com/backtracking/solutions-2/0022-generate-parentheses 来源：算法吧著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

← 「力扣」第 17 题：电话号码的字母组合（中等）「力扣」第 93 题：复原 IP 地址（中等） →