「力扣」第 98 题：验证二叉搜索树（中等）

• 题目链接：98. 验证二叉搜索树 (opens new window)。

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

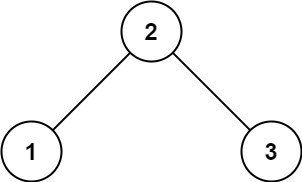
输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -2^31 <= Node.val <= 2^31 - 1

思路分析

二分搜索树定义 3 条，根据定义判断其实是最简单的，在技巧上就是要分一下，是左子树还是右子树。

方法一： 中序遍历判断有序性

说明：这个方法是最容易想到的，直接利用了「二叉搜索树」中序遍历的性质。

参考代码 1：

import java.util.ArrayList;
import java.util.List;

public class Solution {

    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }

        List<Integer> res = new ArrayList<>();
        inOrder(root, res);

        int len = res.size();
        for (int i = 0; i < len - 1; i++) {
            if (res.get(i) >= res.get(i + 1)) {
                return false;
            }
        }
        return true;
    }

    private void inOrder(TreeNode treeNode, List<Integer> res) {
        if (treeNode == null) {
            return;
        }
        inOrder(treeNode.left, res);
        res.add(treeNode.val);
        inOrder(treeNode.right, res);
    }
}

方法二：中序遍历

分析：这个方法知道就可以了。

参考代码 2：

public class Solution2 {

    private long last = Long.MIN_VALUE;

    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }

        if (isValidBST(root.left)) {
            if (last < root.val) {
                last = root.val;
                return isValidBST(root.right);
            }
        }
        return false;
    }
}

方法三：深度优先遍历

即「依据定义」，前序遍历。

参考代码 3：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}


public class Solution {

    public boolean isValidBST(TreeNode root) {
        // 依据定义
        if (root == null) {
            return true;
        }
        return dfs(root.left, root.val, true) &&
                dfs(root.right, root.val, false) &&
                isValidBST(root.left) && isValidBST(root.right);
    }

    /**
     * @param node   当前结点
     * @param val    父亲结点的值
     * @param ifLeft 表示传入的结点是否是左结点
     * @return
     */
    private boolean dfs(TreeNode node, int val, boolean ifLeft) {
        if (node == null) {
            return true;
        }
        if (ifLeft) {
            if (node.val >= val) {
                return false;
            }
            return dfs(node.left, val, true) && dfs(node.right, val, true);
        } else {
            if (node.val <= val) {
                return false;
            }
            return dfs(node.left, val, false) && dfs(node.right, val, false);
        }
    }
}

• 另一种写法

参考代码 4：

public class Solution {

    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        return dfs(root, null, null);
    }

    private boolean dfs(TreeNode node, Integer min, Integer max) {
        if (node == null) {
            return true;
        }
        if (min != null && node.val <= min) {
            return false;
        }
        if (max != null && node.val >= max) {
            return false;
        }
        return dfs(node.left, min, node.val) && dfs(node.right, node.val, max);
    }
}

---

作者：liweiwei1419 链接：https://suanfa8.com/binary-search-tree/solutions/0098-validate-binary-search-tree 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。