算法吧临时网站

# 「力扣」第 15 题：三数之和（中等）

# 题目描述

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 *a，b，c ，*使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意： 答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例 2：

输入：nums = []
输出：[]

示例 3：

输入：nums = [0]
输出：[]

提示：

  • 0 <= nums.length <= 3000

# 思路分析

比较容易想到的思路是 枚举 三数之和的所有情况，时间复杂度为 ，这里 为输入数组的长度。代码如下：

说明：以下代码不能通过。

import java.util.ArrayList;
import java.util.List;

public class Solution {

    public List<List<Integer>> threeSum(int[] nums) {
        int len = nums.length;
        List<List<Integer>> res = new ArrayList<>();
        for (int i = 0; i < len - 2; i++) {
            for (int j = i + 1; j < len - 1; j++) {
                for (int k = j + 1; k < len; k++) {
                    if (nums[i] + nums[j] + nums[k] == 0) {
                        List<Integer> cur = new ArrayList<>(3);
                        cur.add(nums[i]);
                        cur.add(nums[j]);
                        cur.add(nums[k]);
                        res.add(cur);
                    }
                }
            }
        }
        return res;
    }
}

提交以后，出现错误：

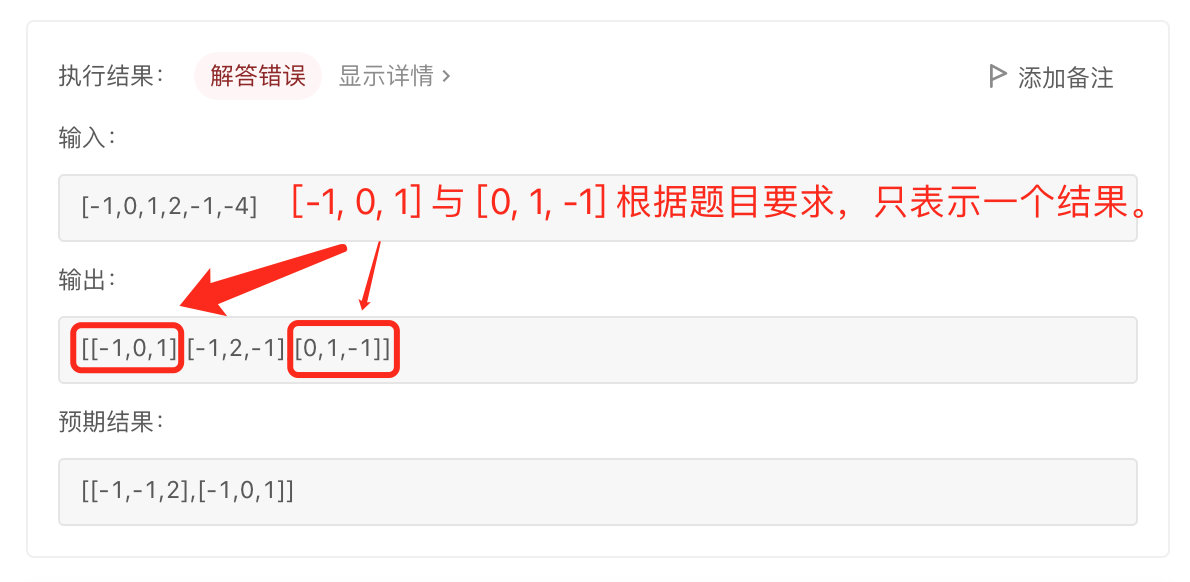
因此需要解决的问题是：如何去掉重复的三元组。

思路 1：使用哈希表。

把得到的三元组放进哈希表去重，大家可以试试看，编码比较麻烦。

思路 2：按照顺序搜索。

这是一个经验。最简单的应用就是从一个数组中找重复元素，排序就可以帮我们方便地找到，因为 重复的元素在排序以后被放在了一起。

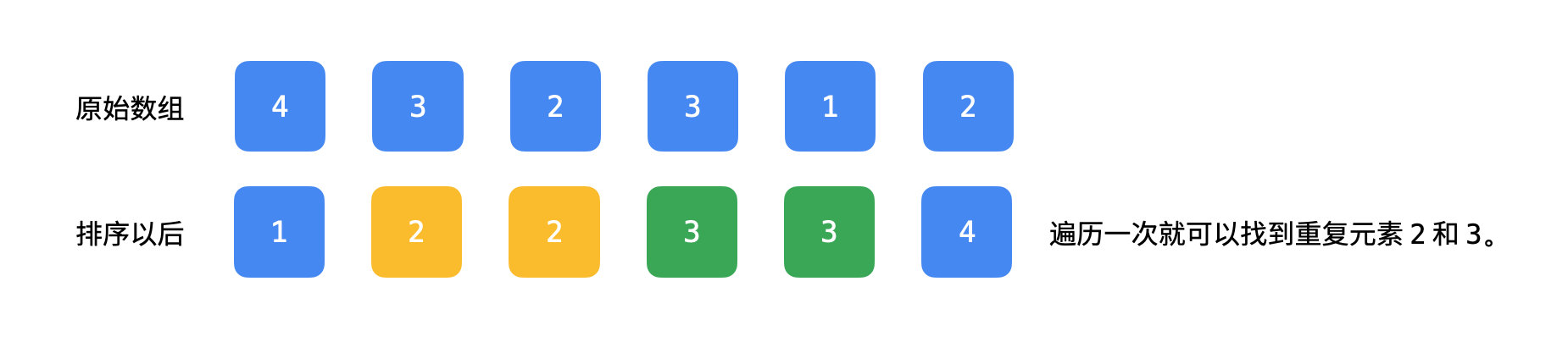
有一些回溯搜索的问题，我们先对输入数组进行排序，可以达到剪枝的效果，提高搜索的效率。

# 方法：双指针

注意：以下叙述的前提是 数组有序。

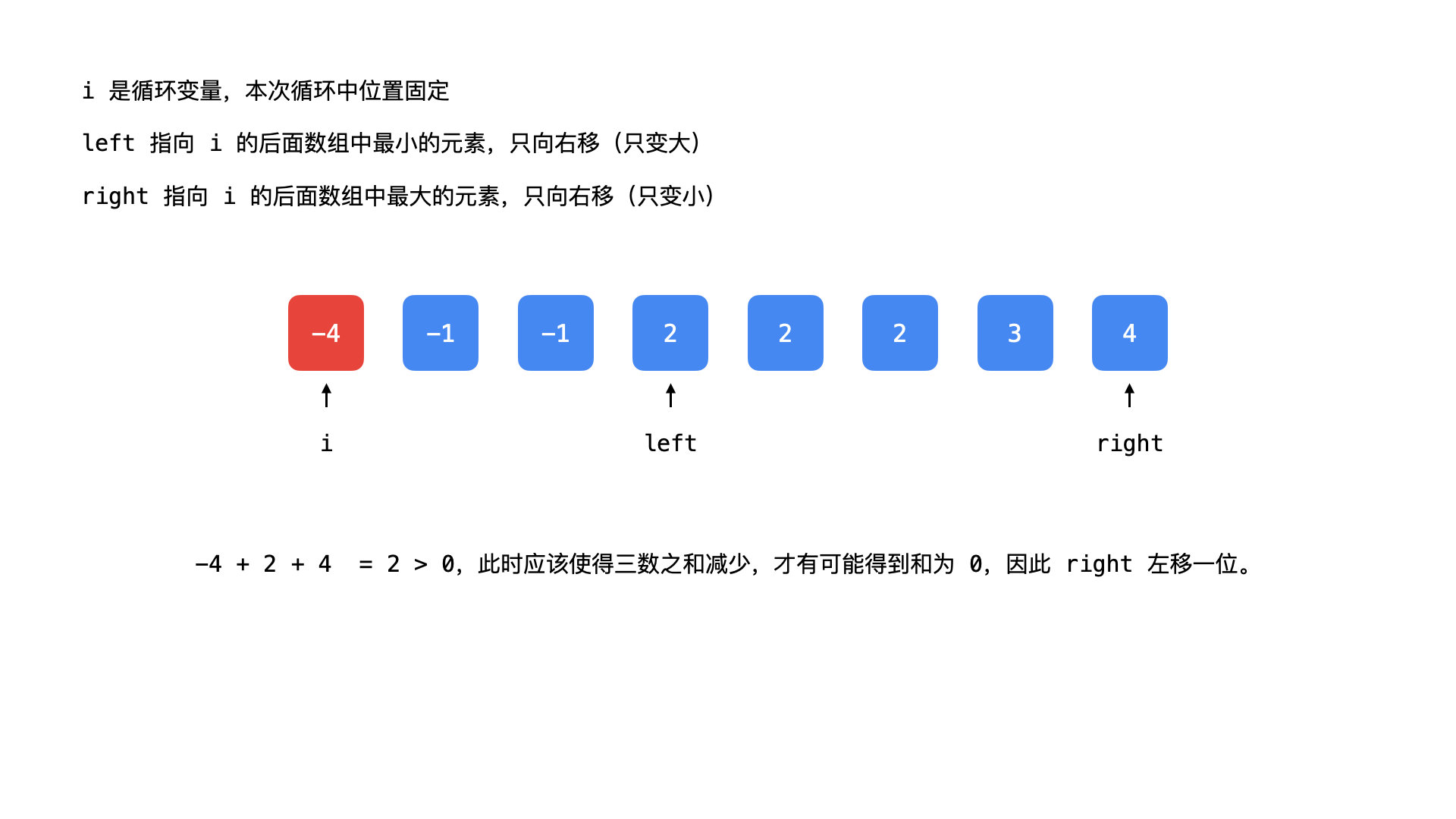
以 为例。下面的幻灯片枚举了 以 作为最小数 的三数之和是如何找到所有解的。

一种办法是枚举，枚举这部分的时间复杂度为 。事实上，可以将时间复杂度降到 。我们只用两个指针变量 left 和 right 分别指向剩下部分的头和尾，即 left 指向最小的数，right 指向最大的数，i 在本轮中固定。

  • 如果 ，说明和太大了，这个时候需要尝试减少三数之和，由于 i 不动，只能 将 right 左移；
  • 如果 ，说明和太小了，这个时候需要尝试增加三数之和，由于 i 不动，只能 将 left 右移；
  • 如果 ，说明找到了一组解。

@slidestart

>

@slideend

# 为什么可以使用「双指针」（重点）？

因为在数组有序的前提下，使用两个指针变量分别位于一个有序区间的头和尾：

  • 如果三数之和较大，应该尝试使得最大值变小，这是因为：
    • 最大值或者最小值变大，三数之和更大；
    • 最小值变小，这种情况在以前已经枚举过；
  • 如果三数之和较小，应该尝试使得最小值变大，这是因为：
    • 最大值或者最小值变小，三数之和更小；
    • 最大值变大，这种情况在以前已经枚举过。

如果这一点还不太清楚的朋友，可以结合上面的幻灯片进行理解。使用「双指针」算法，两个指针变量一头一尾，相向移动，降低了时间复杂度。

下面讲一些细节。

# 细节

  • 由于需要对数组排序，如果枚举的第 1 个数都大于 ，后面的数肯定也大于 ，三数之和肯定大于 ，程序可以终止了；
  • 枚举 i 的时候，如果连续若干个数相等，只需要保留第 1 个数搜索的结果，后面相同的数搜索的结果一定重复，这是因为后面相同的数，搜索的区间是前面的搜索区间的真子集（还是用具体的例子去理解）；
  • left 和 right 相向移动的时候，为了避免搜索到相同的结果，只要找到一组解以后，left 应该右移到和上一次值不同的位置，right 应该左移到和上一次值不同的位置，在代码中分别体现为两个循环语句。

整个代码细节比较多，但其实没有那么难，考虑清楚一些特殊的用例，就不难写出正确的代码。其它细节，我们作为注释写在代码中。

参考代码：

Java 代码：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Solution {

    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        int len = nums.length;
        // 特殊用例判断
        if (len < 3) {
            return res;
        }

        // 排序是去重复的前提
        Arrays.sort(nums);
        // i 枚举到 len - 1 就可以，从 len - 2 开始凑不出 3 个数
        for (int i = 0; i < len - 2; i++) {
            // 因为有序，如果 nums[i] > 0，后面的数一定得不到三数之和为 0
            if (nums[i] > 0) {
                // 注意是 break 不是 continue
                break;
            }

            // 理解这个剪枝非常重要
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            int left = i + 1;
            int right = len - 1;
            // 注意：这里是严格小于，因为要找的是不重合的两个数，当 left 和 right 重合的时候，本轮搜索结束
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];

                if (sum == 0) {
                    List<Integer> cur = new ArrayList<>();
                    cur.add(nums[i]);
                    cur.add(nums[left]);
                    cur.add(nums[right]);
                    res.add(cur);

                    // 剪枝，避免 left 和 right 寻找的过程中出现重复
                    while (left < right && nums[left + 1] == nums[left]) {
                        left++;
                    }
                    while (left < right && nums[right - 1] == nums[right]) {
                        right--;
                    }

                    left++;
                    right--;
                } else if (sum > 0) {
                    // 后面的数太大了，让 right 往左走一步试试看
                    right--;
                } else {
                    // sum < 0， 前面的数太小了，让 left 往右走一步试试看
                    left++;
                }
            }
        }
        return res;
    }

}

Go 代码：

package main

import "sort"

func threeSum(nums []int) [][]int {
  res := make([][]int, 0)
  n := len(nums)
  if n < 3 {
    return res
  }

  sort.Ints(nums)
  for i := 0; i < n-2; i++ {
    if nums[i] > 0 {
      break
    }
    if i > 0 && nums[i] == nums[i-1] {
      continue
    }

    left := i + 1
    right := n - 1
    // 注意：left == right 的时候终止
    for left < right {
      sum := nums[i] + nums[left] + nums[right]
      if sum == 0 {
        res = append(res, []int{nums[i], nums[left], nums[right]})

        for left < right && nums[left+1] == nums[left] {
          left++
        }
        for left < right && nums[right-1] == nums[right] {
          right--
        }
        left++
        right--
      } else if sum > 0 {
        right--
      } else {
        left++
      }
    }
  }
  return res
}

复杂度分析：

  • 时间复杂度：，这里 是输入数组的长度。

    • 排序的时间复杂度为 ；
    • 外层循环枚举 i 的时间复杂度为 ，内层循环使用双指针的时间复杂度为 ，合起来为 。 综合以上两个复杂度 。

# 总结

本题的难点有 2 个：

  • 如何想到通过排序去除重复结果集；
  • 为什么排序以后，可以使用双指针降低时间复杂度。

很多算法问题关键在于想清楚为什么，而不应该只记住解法，分析、解决的过程相当重要。

# 同类问题

作者：liweiwei1419 链接：https://suanfa8.com/two-pointers/solutions-2/0015-3sum 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Last Updated: 11/18/2024, 11:51:07 PM

← 「力扣」第 16 题：最接近的三数之和（中等） →