# 「力扣」第 132 题:分割回文串 II(困难)
# 题目描述
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab"
输出:1
解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。
示例 2:
输入:s = "a"
输出:0
示例 3:
输入:s = "ab"
输出:1
提示:
1 <= s.length <= 2000s仅由小写英文字母组成
# 方法一:动态规划
# 步骤 1:思考状态
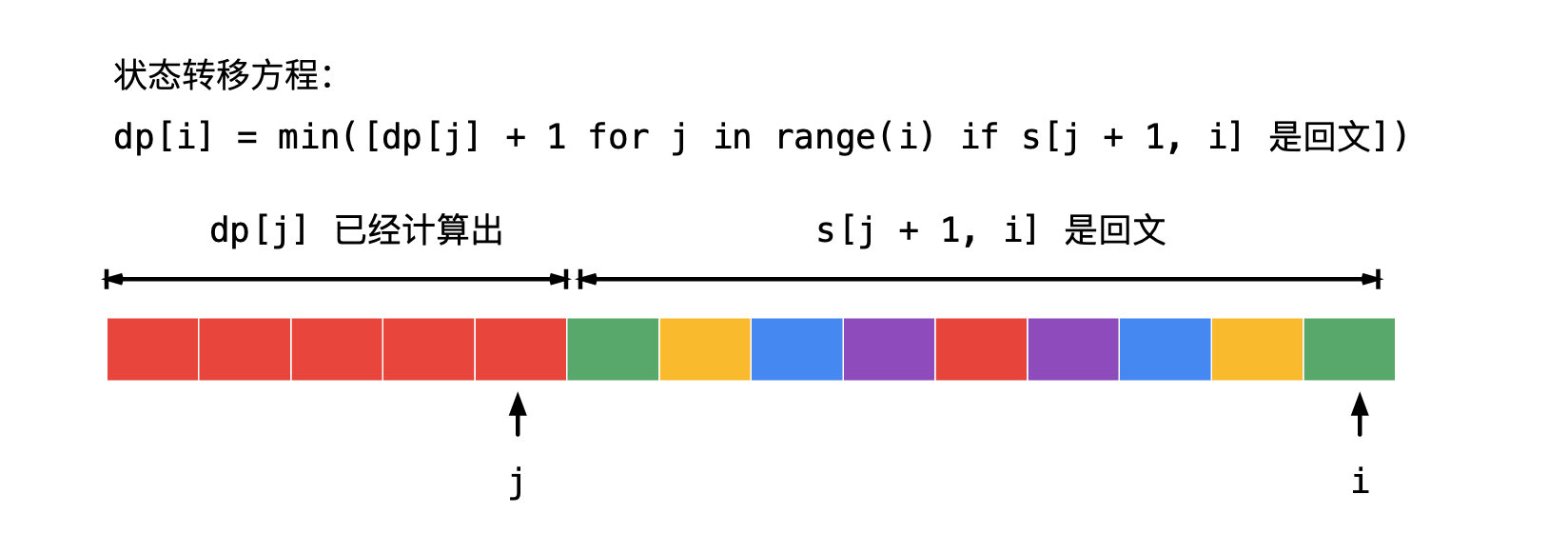
状态就尝试定义成题目问的那样,看看状态转移方程是否容易得到。
dp[i]:表示前缀子串 s[0:i] 分割成若干个回文子串所需要最小分割次数。
# 步骤 2:思考状态转移方程
思考的方向是:大问题的最优解怎么由小问题的最优解得到。
即 dp[i] 如何与 dp[i - 1]、dp[i - 2]、...、dp[0] 建立联系。
比较容易想到的是:如果 s[0:i] 本身就是一个回文串,那么不用分割,即 dp[i] = 0 ,这是首先可以判断的,否则就需要去遍历;
接下来枚举可能分割的位置:即如果 s[0:i] 本身不是一个回文串,就尝试分割,枚举分割的边界 j。
如果 s[j + 1, i] 不是回文串,尝试下一个分割边界。
如果 s[j + 1, i] 是回文串,则 dp[i] 就是在 dp[j] 的基础上多一个分割。
于是枚举 j 所有可能的位置,取所有 dp[j] 中最小的再加 1 ,就是 dp[i]。
得到状态转移方程如下:
dp[i] = min([dp[j] + 1 for j in range(i) if s[j + 1, i] 是回文])
# 步骤 3:思考初始状态
初始状态:单个字符一定是回文串,因此 dp[0] = 0。
# 步骤 4:思考输出
状态转移方程可以得到,并且状态就是题目问的,因此返回最后一个状态即可,即 dp[len - 1]。
# 步骤 5:思考是否可以优化空间
每一个状态值都与之前的状态值有关,因此不能优化空间。
参考代码 1: (Python 代码会超时)
public class Solution {
public int minCut(String s) {
int len = s.length();
if (len < 2) {
return 0;
}
int[] dp = new int[len];
for (int i = 0; i < len; i++) {
dp[i] = i;
}
for (int i = 1; i < len; i++) {
if (checkPalindrome(s, 0, i)) {
dp[i] = 0;
continue;
}
// 当 j == i 成立的时候,s[i] 就一个字符,一定是回文
// 因此,枚举到 i - 1 即可
for (int j = 0; j < i; j++) {
if (checkPalindrome(s, j + 1, i)) {
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
return dp[len - 1];
}
private boolean checkPalindrome(String s, int left, int right) {
while (left < right) {
if (s.charAt(left) != s.charAt(right)) {
return false;
}
left++;
right--;
}
return true;
}
}
class Solution:
def minCut(self, s: str) -> int:
size = len(s)
if size < 2:
return 0
dp = [i for i in range(size)]
for i in range(1, size):
if self.__check_palindrome(s, 0, i):
dp[i] = 0
continue
# 枚举分割点
dp[i] = min([dp[j] + 1 for j in range(i) if self.__check_palindrome(s, j + 1, i)])
return dp[size - 1]
def __check_palindrome(self, s, left, right):
while left < right:
if s[left] != s[right]:
return False
left += 1
right -= 1
return True
Python 代码在面对输入:
"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaabbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
的时候超时。
# 方法二:动态规划(优化)
上面判断回文串的时候方法 checkPalindrome() 是线性的,时间复杂度为
参考代码 2:
public class Solution {
public int minCut(String s) {
int len = s.length();
// 特判
if (len < 2) {
return 0;
}
// 状态定义:dp[i]:前缀子串 s[0:i] (包括索引 i 处的字符)符合要求的最少分割次数
// 状态转移方程:
// dp[i] = min(dp[j] + 1 if s[j + 1: i] 是回文 for j in range(i))
int[] dp = new int[len];
// 2 个字符最多分割 1 次;
// 3 个字符最多分割 2 次
// 初始化的时候,设置成为这个最多分割次数
for (int i = 0; i < len; i++) {
dp[i] = i;
}
// 参考「力扣」第 5 题:最长回文子串 动态规划 的解法
boolean[][] checkPalindrome = new boolean[len][len];
for (int right = 0; right < len; right++) {
// 注意:left <= right 取等号表示 1 个字符的时候也需要判断
for (int left = 0; left <= right; left++) {
if (s.charAt(left) == s.charAt(right) && (right - left <= 2 || checkPalindrome[left + 1][right - 1])) {
checkPalindrome[left][right] = true;
}
}
}
// 1 个字符的时候,不用判断,因此 i 从 1 开始
for (int i = 1; i < len; i++) {
if (checkPalindrome[0][i]){
dp[i] = 0;
continue;
}
// 注意:这里是严格,要保证 s[j + 1:i] 至少得有一个字符串
for (int j = 0; j < i; j++) {
if (checkPalindrome[j + 1][i]) {
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
return dp[len - 1];
}
}
class Solution:
def minCut(self, s: str) -> int:
size = len(s)
if size < 2:
return 0
dp = [i for i in range(size)]
check_palindrome = [[False for _ in range(size)] for _ in range(size)]
for right in range(size):
for left in range(right + 1):
if s[left] == s[right] and (right - left <= 2 or check_palindrome[left + 1][right - 1]):
check_palindrome[left][right] = True
for i in range(1, size):
if check_palindrome[0][i]:
dp[i] = 0
continue
# 枚举分割点
dp[i] = min([dp[j] + 1 for j in range(i) if check_palindrome[j + 1][i]])
return dp[size - 1]
作者:liweiwei1419 链接:https://suanfa8.com/backtracking/solutions-1/0132-palindrome-partitioning-ii 来源:算法吧 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。