「力扣」第 1552 题：两球之间的磁力（中等）

• 题目链接：1552. 两球之间的磁力 (opens new window)。

题目描述

在代号为 C-137 的地球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子，第 i 个篮子的位置在 position[i] ，Morty 想把 m 个球放到这些篮子里，使得任意两球间 最小磁力 最大。

已知两个球如果分别位于 x 和 y ，那么它们之间的磁力为 |x - y| 。

给你一个整数数组 position 和一个整数 m ，请你返回最大化的最小磁力。

示例 1：

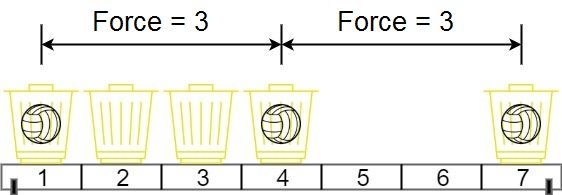
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。

示例 2：

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

提示：

• n == position.length
• 2 <= n <= 10^5
• 1 <= position[i] <= 10^9
• 所有 position 中的整数 互不相同
• 2 <= m <= position.length

题意分析

距离这件事情天然具有连续性，并且距离肯定是正数。并且题目都告诉我们要我们求「最大化的最小磁力」，很显然往「最大值极小化」这一类问题上靠。

分析单调性和左右逼近留给读者。

参考代码：

import java.util.Arrays;

public class Solution {

    public int maxDistance(int[] position, int m) {
        Arrays.sort(position);
        int len = position.length;
        int left = 1;
        int right = position[len - 1] - position[0];

        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (countSplits(position, mid) >= m) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }

    private int countSplits(int[] position, int distance) {
        int len = position.length;
        int pre = position[0];

        int M = 1;
        for (int i = 1; i < len; i++) {
            if (position[i] - pre >= distance) {
                M++;
                pre = position[i];
            }
        }
        return M;
    }
}

---

作者：liweiwei1419 链接：https://suanfa8.com/binary-search/solutions-3/1552-magnetic-force-between-two-balls 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。