「力扣」第 1391 题：检查网格中是否存在有效路径（中等）

• 题目链接：1391. 检查网格中是否存在有效路径 (opens new window)。

题目描述

给你一个 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

• 1 表示连接左单元格和右单元格的街道。
• 2 表示连接上单元格和下单元格的街道。
• 3 表示连接左单元格和下单元格的街道。
• 4 表示连接右单元格和下单元格的街道。
• 5 表示连接左单元格和上单元格的街道。
• 6 表示连接右单元格和上单元格的街道。

你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。

**注意：**你 不能 变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

示例 1：

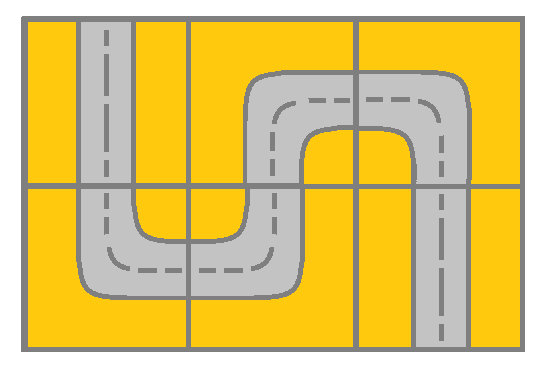
输入：grid = [[2,4,3],[6,5,2]]
输出：true
解释：如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1) 。

示例 2：

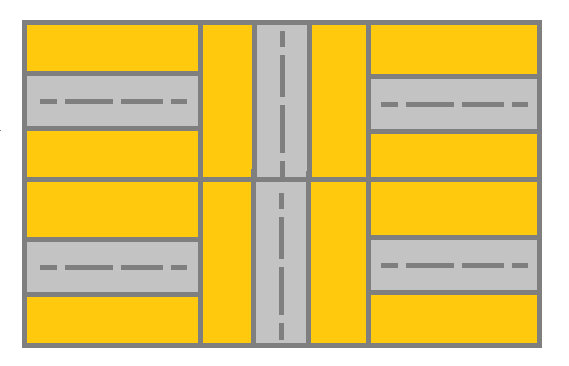
输入：grid = [[1,2,1],[1,2,1]]
输出：false
解释：如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

示例 3：

输入：grid = [[1,1,2]]
输出：false
解释：你会停在 (0, 1)，而且无法到达 (0, 2) 。

示例 4：

输入：grid = [[1,1,1,1,1,1,3]]
输出：true

示例 5：

输入：grid = [[2],[2],[2],[2],[2],[2],[6]]
输出：true

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

方法：深度优先遍历

• 参考题解：C++DFS 解法，容易理解 (opens new window)

public class Solution {

    /**
     * 0 下、1 右、2 上、3 左
     */
    int[] dx = {1, 0, -1, 0};
    int[] dy = {0, 1, 0, -1};

    public boolean hasValidPath(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        visited = new boolean[m][n];

        // 起点的拼图编号
        int start = grid[0][0];

        // 朝着四个方向都试一下
        for (int i = 0; i < 4; ++i) {
            // 当前方向可以走
            if (pipe[start][i] != -1) {
                if (dfs(0, 0, pipe[start][i], grid)) {
                    return true;
                }
            }
        }
        return false;
    }

    private int m;
    private int n;

    /**
     * 总共就 6 种拼图，所以下标到 6
     */
    int[][] pipe = {
            {-1, -1, -1, -1},
            {-1, 1, -1, 3},
            {0, -1, 2, -1},
            {-1, 0, 3, -1},
            {-1, -1, 1, 0},
            {3, 2, -1, -1},
            {1, -1, -1, 2}
    };

    /**
     * 记录各个拼图块路径的方向，0、1、2、3代表方向，-1 代表不可走
     */
    private boolean[][] visited;

    private boolean dfs(int x, int y, int dir, int[][] grid) {
        visited[x][y] = true;
        if (x == m - 1 && y == n - 1) {
            // 到达终点
            return true;
        }

        // 得到下一个准备走的坐标
        int newX = x + dx[dir];
        int newY = y + dy[dir];
        if (newX < 0 || newY < 0 || newX >= m || newY >= n) {
            // 越界
            return false;
        }
        // 得到下一块拼图的编号
        int nxt = grid[newX][newY];
        if (pipe[nxt][dir] != -1 && !visited[newX][newY]) {
            // 如果当前方向可走，则方向改变，继续走
            return dfs(newX, newY, pipe[nxt][dir], grid);
        }
        return false;
    }
}

---

作者：liweiwei1419 链接：https://suanfa8.com/backtracking/solutions-3/1391-check-if-there-is-a-valid-path-in-a-grid 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。