# 「力扣」第 1631 题:最小体力消耗路径(中等)
# 题目描述
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
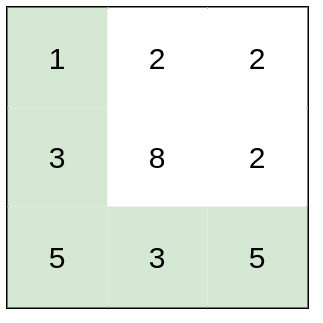
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:

输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
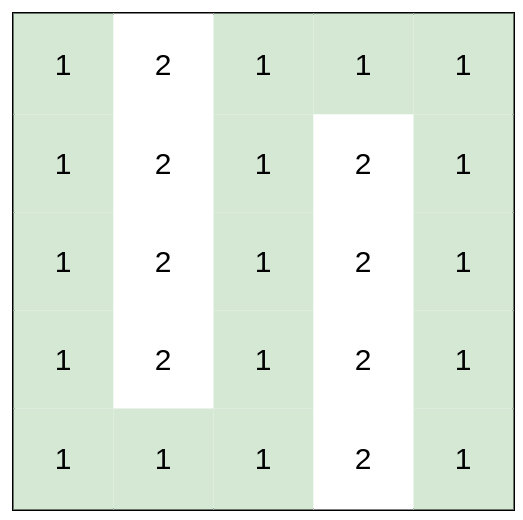
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 106
# 方法一:二分查找 + DFS
参考代码 1:
public class Solution {
private int rows;
private int cols;
private static final int[][] DIRECTIONS = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int minimumEffortPath(int[][] heights) {
rows = heights.length;
cols = heights[0].length;
if (rows == 1 && cols == 1) {
return 0;
}
// 1 <= heights[i][j] <= 10^6
int left = 0;
int right = 999999;
while (left < right) {
// 不会溢出,因此不用写成 left + (right - left) / 2
int mid = (left + right) / 2;
boolean[][] visited = new boolean[rows][cols];
if (dfs(heights, mid, 0, 0, visited)) {
// mid 是符合要求的,下一轮搜索区间 [left..mid]
right = mid;
} else {
// 下一轮搜索区间 [mid + 1, right]
left = mid + 1;
}
}
return left;
}
/**
* 如果遍历到的路径的所有路径差都小于等于 diff,返回 true
*
* @param heights
* @param diff
* @param x
* @param y
* @param visited
* @return
*/
private boolean dfs(int[][] heights, int diff, int x, int y, boolean[][] visited) {
visited[x][y] = true;
for (int[] direction : DIRECTIONS) {
int newX = x + direction[0];
int newY = y + direction[1];
// 只要扩展下去,有一个方向的的单元格数值与当前单元格数值的绝对值 <= diff ,就继续深度优先遍历
if (inArea(newX, newY) && !visited[newX][newY] && Math.abs(heights[newX][newY] - heights[x][y]) <= diff) {
// 递归终止条件:走到了最后一个单元格
if (newX == rows - 1 && newY == cols - 1) {
return true;
}
if (dfs(heights, diff, newX, newY, visited)) {
return true;
}
}
}
// 4 个方向深搜完以后,发现都有 > diff 的路径,才返回 false
return false;
}
private boolean inArea(int x, int y) {
return x >= 0 && x < rows && y >= 0 && y < cols;
}
}
# 方法二:二分查找 + BFS
参考代码 2:
import java.util.LinkedList;
import java.util.Queue;
public class Solution {
private int rows;
private int cols;
private static final int[][] DIRECTIONS = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int minimumEffortPath(int[][] heights) {
rows = heights.length;
cols = heights[0].length;
if (rows == 1 && cols == 1) {
return 0;
}
int left = 0;
int right = 999999;
while (left < right) {
// 不会溢出,因此不用写成 left + (right - left) / 2
int mid = (left + right) / 2;
boolean[][] visited = new boolean[rows][cols];
if (bfs(heights, mid, 0, 0, visited)) {
// mid 是符合要求的,下一轮搜索区间 [left..mid]
right = mid;
} else {
// 下一轮搜索区间 [mid + 1..right]
left = mid + 1;
}
}
return left;
}
/**
* 如果遍历到的路径的所有路径差都小于等于 diff,返回 true
*
* @param heights
* @param diff
* @param x
* @param y
* @param visited
* @return
*/
private boolean bfs(int[][] heights, int diff, int x, int y, boolean[][] visited) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{x, y});
visited[x][y] = true;
while (!queue.isEmpty()) {
int[] front = queue.poll();
for (int[] direction : DIRECTIONS) {
int newX = front[0] + direction[0];
int newY = front[1] + direction[1];
if (inArea(newX, newY) && !visited[newX][newY] && Math.abs(heights[newX][newY] - heights[front[0]][front[1]]) <= diff) {
if (newX == rows - 1 && newY == cols - 1) {
return true;
}
queue.offer(new int[]{newX, newY});
visited[newX][newY] = true;
}
}
}
return false;
}
private boolean inArea(int x, int y) {
return x >= 0 && x < rows && y >= 0 && y < cols;
}
}
作者:liweiwei1419 链接:https://suanfa8.com/backtracking/solutions-3/1631-path-with-minimum-effort 来源:算法吧 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。