算法吧临时网站

# 「力扣」第 452 题：用最少数量的箭引爆气球（中等）

# 题目描述

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 ，，且满足 ，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 ，其中 ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：

输入:
[[10,16], [2,8], [1,6], [7,12]]

输出:
2

解释:
对于该样例，我们可以在x = 6（射爆[2,8],[1,6]两个气球）和 x = 11（射爆另外两个气球）。

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2

示例 4：

输入：points = [[1,2]]
输出：1

示例 5：

输入：points = [[2,3],[2,3]]
输出：1

提示：

思路分析：对于一些物理的问题、画面感比较强的问题，例如当前需要解决的区间问题，我们建议大家通过研究示例，在草稿纸上画出示意图，打开思路。

我们将示例 1 所示的情况在草稿纸上画出示意图，这里为了示意方便，我们将一只气球使用一个区间表示。图中红色区域是不同区间的交集，在红色区域使用一支箭会击穿较多气球。

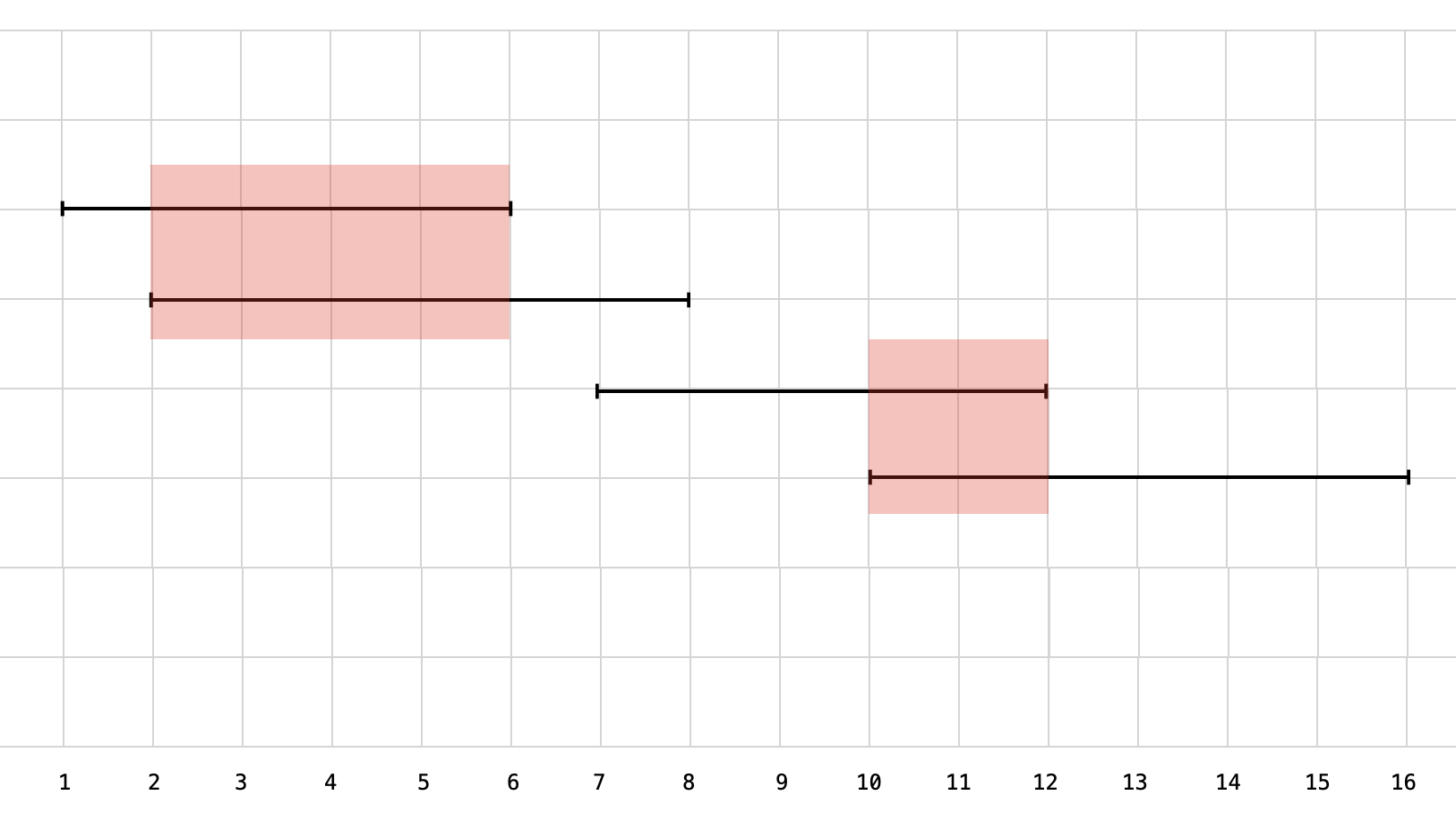
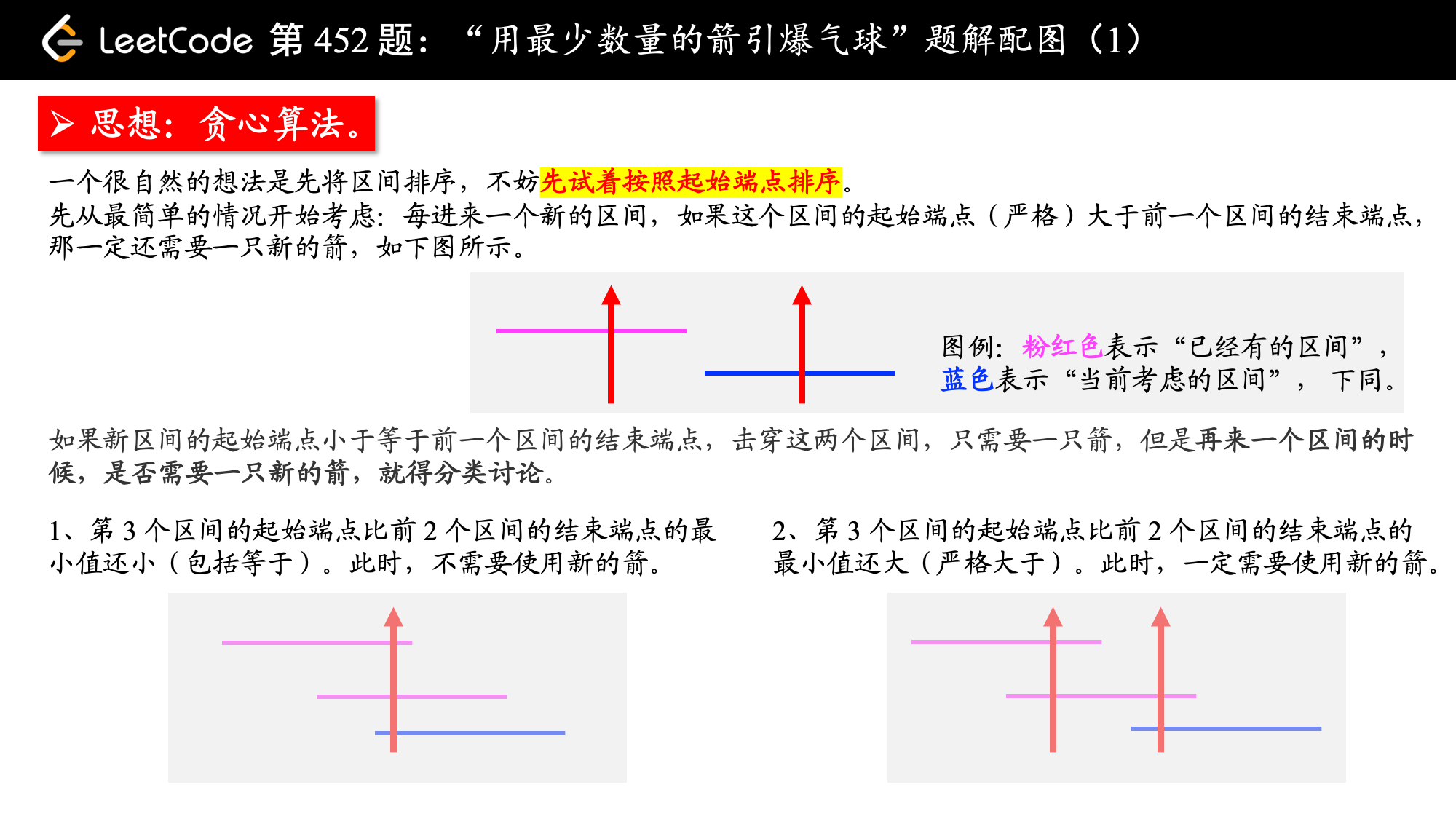
# 「贪心算法」的直觉

可以发现，如果两个气球（区间）有公共的部分（根据示例 2 和示例 3，有公共部分包括区间端点重合），我们可以使用一支箭将它们击穿。因此我们希望如果这些气球表示的区间的重合部分越多，那么我们需要使用的箭的数量就越少。因此贪心的地方是：区间重合的部分越多越好。在计算结果的时候，如果若干个区间有交集，它们只记录 。

计算若干个区间的交集，我们需要对区间进行排序。我们「按照区间的左端点升序排序」和「按照区间的右端点升序排序」这两种方式都试试。

# 方法一：按照区间的左端点升序排序

  • 此时左端点已经升序排序，为此我们需要关注的是新遍历到的区间的右端点和已经遍历到的区间的右端点的最小值（因为需要取交集）；
  • 如果新遍历到的区间的左端点 严格大于 之前遍历到的区间的右端点，说明此时需要新使用一支箭，否则说明两个区间有交集，此时不需要新使用一支箭。

参考代码：

import java.util.Arrays;
import java.util.Comparator;

public class Solution {

    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if (len < 2) {
            return len;
        }

        Arrays.sort(points, Comparator.comparingInt(o -> o[0]));
        int res = 1;

        // 当前区间的结尾下标
        int end = points[0][1];
        for (int i = 1; i < len; i++) {
            if (points[i][0] > end) {
                res++;
                end = points[i][1];
            } else {
                end = Math.min(end, points[i][1]);
            }
        }
        return res;
    }
}

复杂度分析：

  • 时间复杂度：，时间复杂度主要集中在排序方法上，之后遍历数组的时间复杂度为 ，此时 ；
  • 空间复杂度：，假设排序方法为快速排序，排序方法需要使用的空间大小为 。

# 方法二：按照区间的右端点升序排序

  • 此时右端点已经升序排序，为此我们需要关注的是新遍历到的区间的左端点；
  • 如果当前新遍历到的新区间的左端点 严格大于 之前遍历到的区间的右端点（区间已经按照右端点升序排序），此时就需要新使用一支箭，否则说明两个区间有交集，此时不需要新使用一支箭。

参考代码：

import java.util.Arrays;
import java.util.Comparator;

public class Solution {

    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if (len < 2) {
            return len;
        }

        Arrays.sort(points, Comparator.comparingInt(o -> o[1]));
        int end = points[0][1];
        int res = 1;
        for (int i = 1; i < len; i++) {
            if (points[i][0] > end) {
                end = points[i][1];
                res++;
            }
        }
        return res;
    }
}

复杂度分析：（同参考代码 1）

# 贪心算法（Python 代码、Java 代码）

解题关键：画图。

根据以上讨论，我们可以设置一个 end 标记， 它表示：在遍历的过程中使用当前这只箭能够击穿所有气球的最远距离。这个最远距离，在每遍历一个新区间的时候，都会检查一下，取最小值。

根据以上分析，不难写出下面的代码：

参考代码：

Java 代码：

import java.util.Arrays;
import java.util.Comparator;

public class Solution {

    public int findMinArrowShots(int[][] points) {
        int plen = points.length;
        if (plen < 2) {
            return plen;
        }

        // 按照起点进行排序
        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0] != o2[0]) {
                    return o1[0] - o2[0];
                }
                return o1[1] - o2[1];
            }
        });

        // 最少的数量
        int minCount = 1;
        // 第 1 个区间的末尾，目前线段能够达到的最远位置
        int end = points[0][1];
        // 贪心法，基于上一个箭，记录当前能够射穿的所有的区间
        for (int i = 1; i < plen; i++) {
            if (points[i][0] <= end) {
                end = Math.min(end, points[i][1]);
            } else {
                minCount++;
                end = points[i][1];
            }
        }
        return minCount;
    }
}

Python 代码：

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        size = len(points)
        # 特判
        if size < 2:
            return size
        # 按照区间的起始端点排序
        points.sort(key=lambda x:x[0])

        # 只要有区间就至少需要一只箭
        res = 1
        # 最远距离：使用当前这只箭能引爆气球的最远距离
        end = points[0][1]

        for i in range(1, size):
            if points[i][0] > end:
                end = points[i][1]
                res += 1
            else:
                end = min(end, points[i][1])
        return res

这一版代码提交就已经可以通过了。我们想一想还能不能写得更好一些。经过上面的分析，我们发现，区间的末尾端点很重要：如果不使用新的箭，新区间末尾端点就要和当前的“最远距离”（含义通过上文可以明白）作一个比较，取最小值。那我不妨就按照区间的末尾端点排序，这样如果不使用新的箭，也不用作比较了，比起上面的代码来说，就少了一个分支。

（如果上面的叙述不好理解的话，可以在草稿纸上多画几条线段，就很清楚了。）

参考代码：

Java 代码：

import java.util.Arrays;
import java.util.Comparator;

public class Solution {
    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if (len < 2) {
            return len;
        }

        // 按照区间终点进行排序
        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] point1, int[] point2) {
                if (point1[1] != point2[1]) {
                    return point1[1] - point2[1];
                }
                return point1[0] - point2[0];
            }
        });

        int count = 1;
        int end = points[0][1];
        for (int i = 1; i < len; i++) {
            if (points[i][0] > end) {
                // 就得多用一支箭
                end = points[i][1];
                count++;
            }
        }
        return count;
    }
}

Python 代码：

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        size = len(points)
        if size < 2:
            return size

        # 按照区间的末尾端点排序
        points.sort(key=lambda x:x[1])
        res = 1
        # 最远距离：使用当前这只箭能引爆气球的最远距离
        end = points[0][1]

        for i in range(1, size):
            if points[i][0] > end:
                end = points[i][1]
                res += 1
        return res

复杂度分析：

  • 时间复杂度：： 为气球的个数，时间复杂度为排序算法的时间复杂度，感谢用户 @powerboy6 提供的评论；
  • 空间复杂度：。

作者：liweiwei1419 链接：https://suanfa8.com/greedy/solutions/0452-minimum-number-of-arrows-to-burst-balloons 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Last Updated: 11/19/2024, 11:31:47 AM

← 「力扣」第 455 题：分发饼干（中等） →