# 「力扣」第 45 题:跳跃游戏 II(困难)
# 题目描述
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 10^40 <= nums[i] <= 1000
# 方法一:广度优先遍历
题目问的是「最少跳跃次数」,这很容易让我们想到使用「广度优先遍历」求解。该问题可以建模成为一个图论的问题,因此需要借助队列和哈希表(防止重复访问)。
参考代码 1:
import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Set;
public class Solution {
public int jump(int[] nums) {
int len = nums.length;
if (len < 2) {
return 0;
}
Queue<Integer> queue = new LinkedList<>();
Set<Integer> hashSet = new HashSet<>();
queue.add(0);
int target = len - 1;
int minStep = 0;
while (!queue.isEmpty()) {
int currentSize = queue.size();
for (int i = 0; i < currentSize; i++) {
Integer head = queue.poll();
if (head == target) {
return minStep;
}
for (int j = head + 1; j <= Math.min(head + nums[head], len - 1); j++) {
if (hashSet.contains(j)) {
continue;
}
queue.add(j);
hashSet.add(j);
}
}
minStep++;
}
return minStep;
}
}
复杂度分析:
- 时间复杂度:
,这里 是输入数组的长度,对于遍历到的每一个位置,广度优先遍历算法考虑了每一种可以跳跃的情况,每一个位置的后面需要考虑的位置的数量为 ; - 空间复杂度:
,哈希表的大小为 ,最差情况下,队列的长度为 ,总共需要 大小的空间。
事实上,既然要求的是「最少跳跃次数」,就要求我们:如果能够到达一个位置能选择跳 1 次绝对不应该选择跳 2 次,能选择跳 2 次绝对不应该选择跳 3 次。
# 方法二:贪心算法
分析题目中仅有的示例:
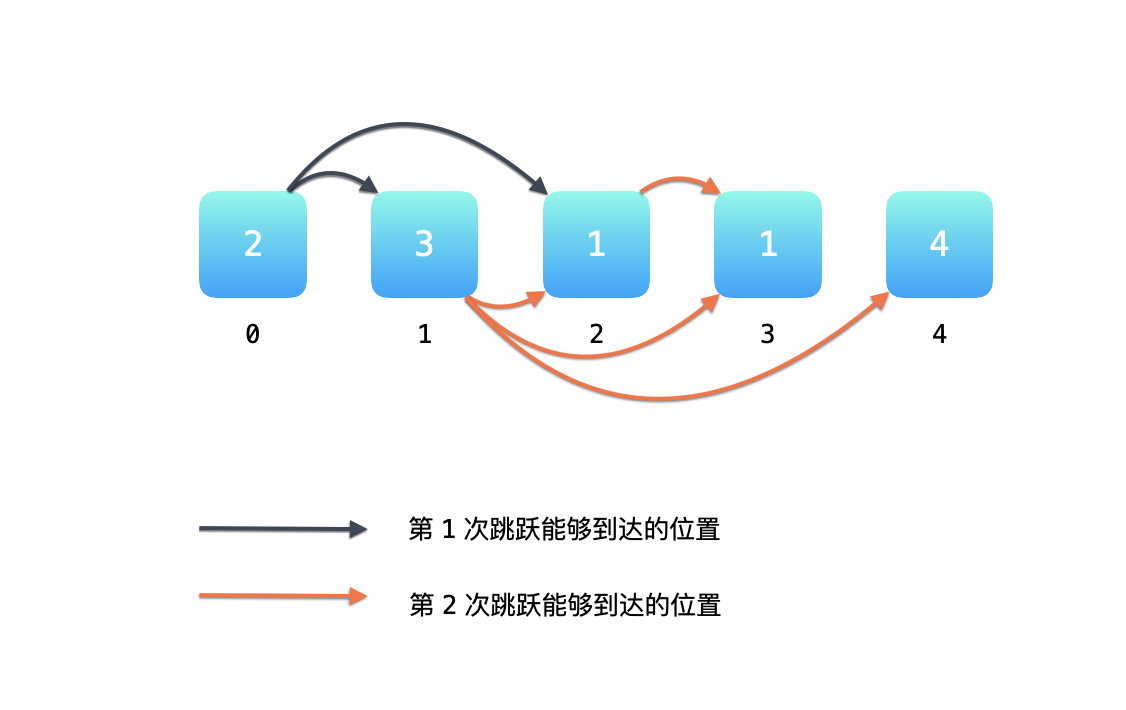
- 第 1 次跳跃可以到达的位置是下标 1 和下标 2;
- 第 2 次跳跃可以到达的位置是下标 2 、下标 3 和下标 4。
「贪心算法」的直觉:
如果我们想达到下标 2,一定只会选择跳 1 次(从下标 0 跳到下标 2,图中黑色箭头),而不会选择跳 2 次(从下标 0 跳到下标 1,再从下标 1 跳到下标 2,图中黑色箭头加红色箭头)。
所以,从起点位置(下标 0)只跳跃 1 次,最多可以跳到的位置是下标 2。
- 现在考虑下标位置 3,由于第 1 次跳跃最多只能跳到下标 2,因此到达下标 3 位置最少需要跳 2 次;
- 现在考虑下标位置 4,由于第 1 次跳跃最多只能跳到下标 2,因此到达下标 4 位置最少需要跳 2 次。
所以,从起点位置(下标 0)只跳跃 2 次,最多可以跳到的位置是下标 4,如果有下标 5,那么达到下标 5 最少需要跳 3 次,如下图所示。
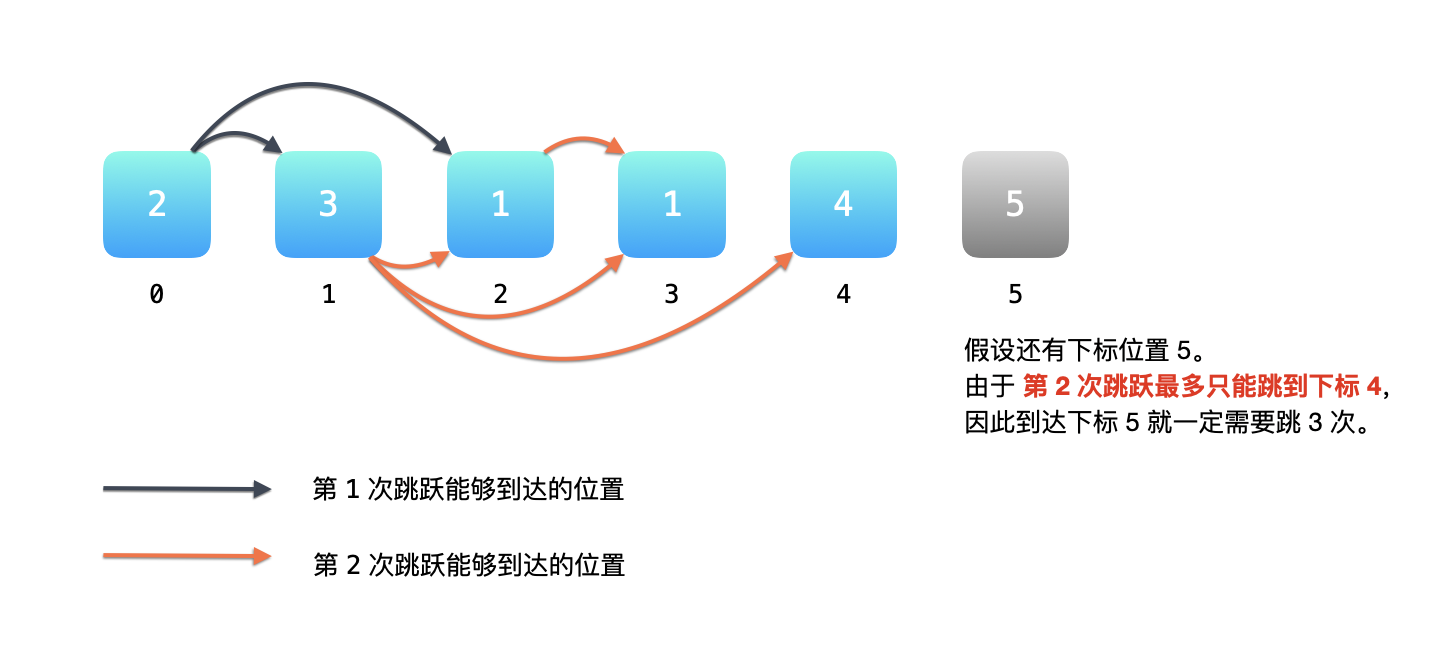
因此,我们除了关心「当前步骤可以跳到的最远的位置」以外,还需要关心「下一步跳跃可以到达的最远的位置」(这一点是可以「贪心选择性质」)。如果比较难理解,可以再对照上图,虚拟出来的灰色结点 5,想一想为什么从起点位置(下标 0)到灰色结点 5,最少需要跳 3 次。
因此,我们除了关心从当前位置跳一步可以到达的最远位置以外,还需要关心从当前位置跳两步可以到达的最远的位置。
参考代码 2:
public class Solution {
public int jump(int[] nums) {
int len = nums.length;
int currMaxReached = 0;
int nextMaxReached = 0;
int res = 0;
// 最后一个位置不用看
for (int i = 0; i < len - 1; i++) {
nextMaxReached = Math.max(nextMaxReached, nums[i] + i);
if (i == currMaxReached) {
// 遇到这一步可以到达的最远边界,就更新为下一步可以达到的最远边界,并且最少步数加一
currMaxReached = nextMaxReached;
res++;
}
}
return res;
}
}
复杂度分析:
- 时间复杂度:
,这里 是输入数组的长度,遍历了输入数组一次,每遍历一个元素只考虑维护了 currMaxReached和nextMaxReached; - 空间复杂度:
。
作者:liweiwei1419 链接:https://suanfa8.com/greedy/solutions/0045-jump-game-ii 来源:算法吧 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。