「力扣」第 1559 题：二维网格图中探测环（中等）

• 题目链接： 1559. 二维网格图中探测环 (opens new window)。

题目描述

给你一个二维字符网格数组 grid ，大小为 m x n ，你需要检查 grid 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值 。

同时，你也不能回到上一次移动时所在的格子。比方说，环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。

如果 grid 中有相同值形成的环，请你返回 true ，否则返回 false 。

示例 1：

输入：grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
输出：true
解释：如下图所示，有 2 个用不同颜色标出来的环：

示例 2：

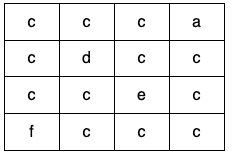
输入：grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
输出：true
解释：如下图所示，只有高亮所示的一个合法环：

示例 3：

输入：grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
输出：false

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m <= 500
• 1 <= n <= 500
• grid 只包含小写英文字母。

说明：因时间和精力关系，本题没有写详解，只给出了参考代码。读者可以在「力扣」这道题的评论区和题解区找到适合自己的思路分析和代码。如果确实需要我编写具体的解题思路，可以发邮件到 liweiwei1419@gmail.com。

方法一：并查集

参考代码：

public class Solution {

    private int rows;
    private int cols;

    public boolean containsCycle(char[][] grid) {
        rows = grid.length;
        cols = grid[0].length;
        int[][] directions = new int[][]{{1, 0}, {0, 1}};
        UnionFind unionFind = new UnionFind(cols * rows);
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < cols; ++j) {
                char current = grid[i][j];
                for (int[] direction : directions) {
                    int newX = i + direction[0];
                    int newY = j + direction[1];
                    if (inArea(newX, newY) && current == grid[newX][newY]) {
                        if (unionFind.union(getIndex(i, j), getIndex(newX, newY))) {
                            return true;
                        }
                    }
                }
            }
        }
        return false;
    }

    private boolean inArea(int x, int y) {
        return 0 <= x && x < rows && 0 <= y && y < cols;
    }

    private int getIndex(int x, int y) {
        return x * cols + y;
    }

    private class UnionFind {

        private int[] parent;

        public UnionFind(int N) {
            parent = new int[N];
            for (int i = 0; i < N; ++i) {
                parent[i] = i;
            }
        }

        private int find(int x) {
            if (parent[x] != x) {
                // 完全压缩
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }

        /**
         * @param x
         * @param y
         * @return 如果在同一个集合中，返回 true
         */
        public boolean union(int x, int y) {
            int parentX = find(x);
            int parentY = find(y);
            if (parentX == parentY) {
                return true;
            }
            if (parentX < parentY) {
                parent[parentY] = parentX;
            } else {
                parent[parentX] = parentY;
            }
            return false;
        }
    }
}

方法二：深度优先遍历

参考代码：

public class Solution {

    private char[][] grid;
    private int cols;
    private int rows;

    private boolean[][] visited;
    private int[][] directions = new int[][]{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    // DFS 的写法

    public boolean containsCycle(char[][] grid) {
        if (grid.length == 0) {
            return false;
        }
        this.grid = grid;
        rows = grid.length;
        cols = grid[0].length;
        visited = new boolean[rows][cols];

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (!visited[i][j] && dfs(new int[]{i, j}, null)) {
                    return true;
                }
            }
        }
        return false;
    }


    private boolean dfs(int[] current, int[] pre) {
        if (visited[current[0]][current[1]]) {
            return true;
        }

        boolean res = false;
        visited[current[0]][current[1]] = true;
        char target = grid[current[0]][current[1]];

        for (int[] dir : directions) {
            int nextX = current[0] + dir[0];
            int nextY = current[1] + dir[1];
            if (inArea(nextX, nextY)
                    && grid[nextX][nextY] == target
                    && (pre == null || nextX != pre[0] || nextY != pre[1])) {
                res = dfs(new int[]{nextX, nextY}, current);
            }
            if (res) {
                break;
            }
        }
        return res;
    }

    private boolean inArea(int x, int y) {
        return 0 <= x && x < rows && 0 <= y && y < cols;
    }

    private int getIndex(int x, int y) {
        return x * cols + y;
    }
}

---

作者：liweiwei1419 链接：https://suanfa8.com/union-find/solutions/1559-detect-cycles-in-2d-grid 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。