「力扣」第 105 题：从前序与中序遍历序列构造二叉树（中等）

• 题目链接：105. 从前序与中序遍历序列构造二叉树 (opens new window)；
• 题解链接：
  • 官方题解（含视频题解） (opens new window)；
  • 分治法（Python 代码、Java 代码）（含视频讲解） (opens new window)。这个题解里面的视频是我最早录的视频，效果不好，可以不用看。

题目描述

给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均无重复元素
• inorder 均出现在 preorder
• preorder 保证为二叉树的前序遍历序列
• inorder 保证为二叉树的中序遍历序列

温馨提示：这道题大家可以看 官方题解 (opens new window) 下的视频或者 B 站 (opens new window) 的视频，加速播放不影响理解。

思路分析

• 树相关的问题的解决思路都有「分治思想」在里面。分治思想：把原问题拆解成若干个与原问题结构相同但规模更小的子问题，待子问题解决以后，原问题就得以解决。「归并排序」和「快速排序」都是分治思想的应用，其中「归并排序」先无脑地「分」，在「合」的时候就麻烦一些；「快速排序」开始在 partition （划分）上花了很多时间，然后就递归处理下去就好了，没有在「合」上再花时间。
• 这道题的重点在于：「前序遍历序列」的第 1 个元素一定是二叉树的根结点，于是可以在「中序遍历序列」中找这个根结点的下标，然后把「前序遍历序列」和「中序遍历序列」分为两个部分，分别对应二叉树的左子树和右子树，分别递归完成就可以了。拿题目给出的例子画一个图，思路就打开了。

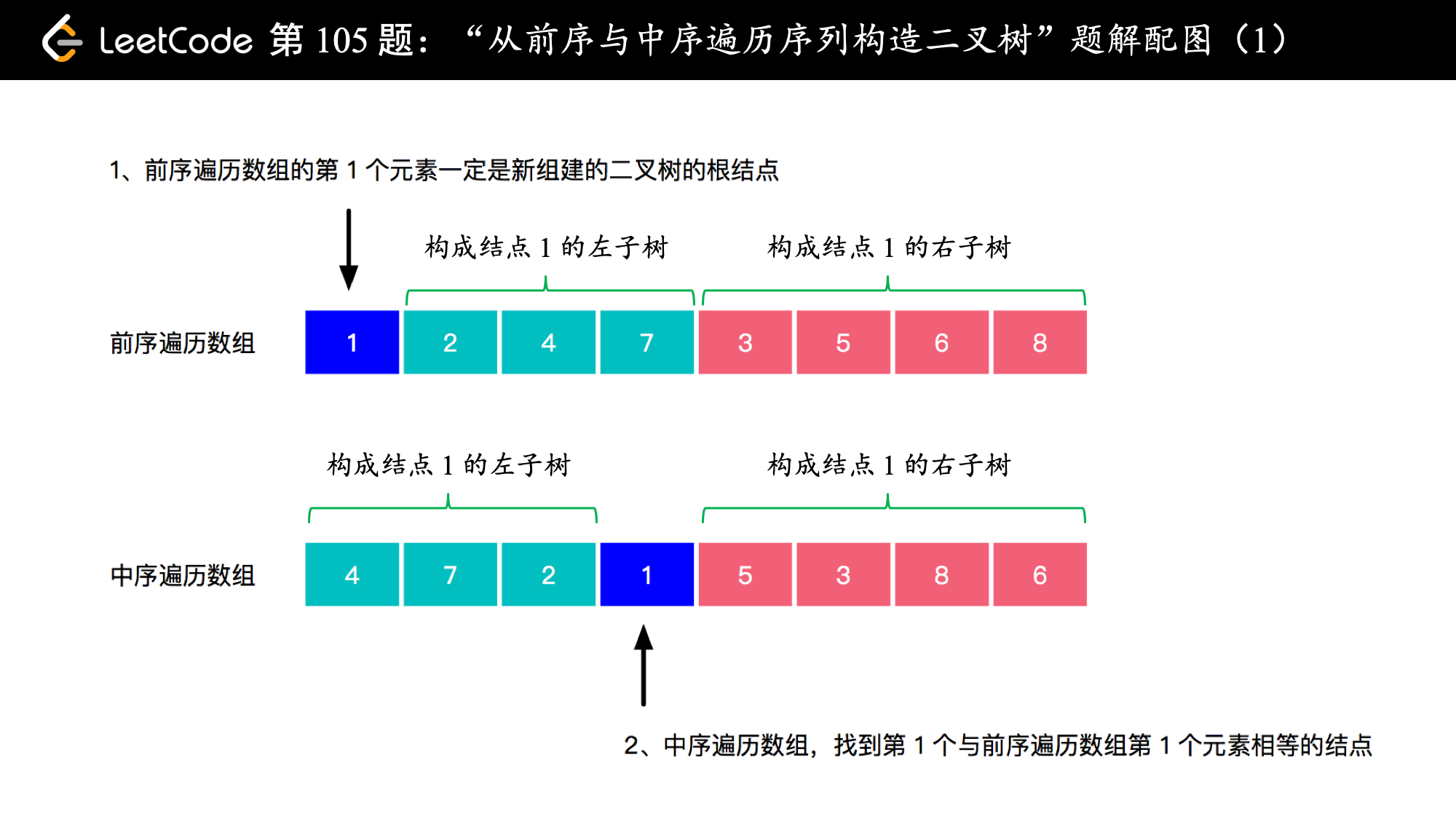
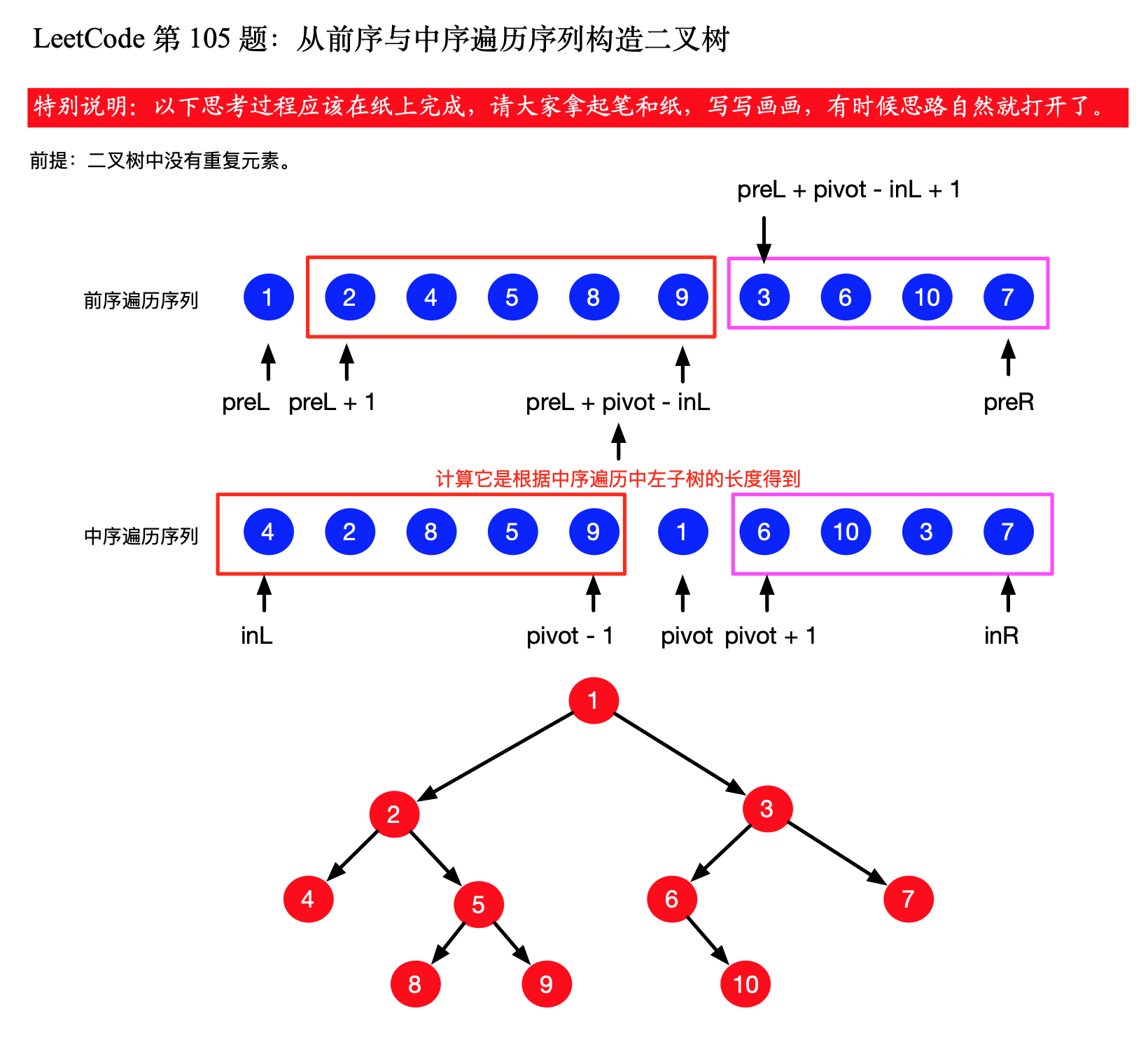
下面是一个具体的例子，演示了如何计算数组子区间的左右边界：

这道题完成了以后可以把 「力扣」 第 106 题：从中序与后序遍历序列构造二叉树 (opens new window) 一起做了。

优化（重点）

可以将中序遍历的值和下标存在一个哈希表中（键：数值，值：下标），这样就可以根据数值一下子找到当前根结点在中序遍历序列中的下标（前提：二叉树中没有重复元素，题目的数据范围里有讲到）。如果不这样做的话，时间复杂度会增加。

参考代码：

import java.util.HashMap;
import java.util.Map;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

public class Solution {

    private int[] preorder;
    private Map<Integer, Integer> hash;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int preLen = preorder.length;
        int inLen = inorder.length;
        if (preLen != inLen) {
            throw new RuntimeException("Incorrect input data.");
        }
        this.preorder = preorder;
        this.hash = new HashMap<>();
        for (int i = 0; i < inLen; i++) {
            hash.put(inorder[i], i);
        }

        return buildTree(0, preLen - 1, 0, inLen - 1);
    }


    private TreeNode buildTree(int preLeft, int preRight, int inLeft, int inRight) {
        // 因为是递归调用的方法，按照国际惯例，先写递归终止条件
        if (preLeft > preRight || inLeft > inRight) {
            return null;
        }
        // 先序遍历的起点元素很重要
        int pivot = preorder[preLeft];
        TreeNode root = new TreeNode(pivot);
        int pivotIndex = hash.get(pivot);
        root.left = buildTree(preLeft + 1, pivotIndex - inLeft + preLeft,
                inLeft, pivotIndex - 1);
        root.right = buildTree(pivotIndex - inLeft + preLeft + 1, preRight,
                pivotIndex + 1, inRight);
        return root;
    }
}

复杂度分析：

• 时间复杂度：，这里 是二叉树的结点个数，每调用一次递归方法创建一个结点，一共创建 个结点；
• 空间复杂度：，这里忽略递归方法占用的空间，。

---

作者：liweiwei1419 链接：https://suanfa8.com/tree/solutions/0105-construct-binary-tree-from-preorder-and-inorder-traversal 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。