「力扣」第 863 题：二叉树中所有距离为 K 的结点（中等）

• 题目链接：863. 二叉树中所有距离为 K 的结点 (opens new window)。

题目描述

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1

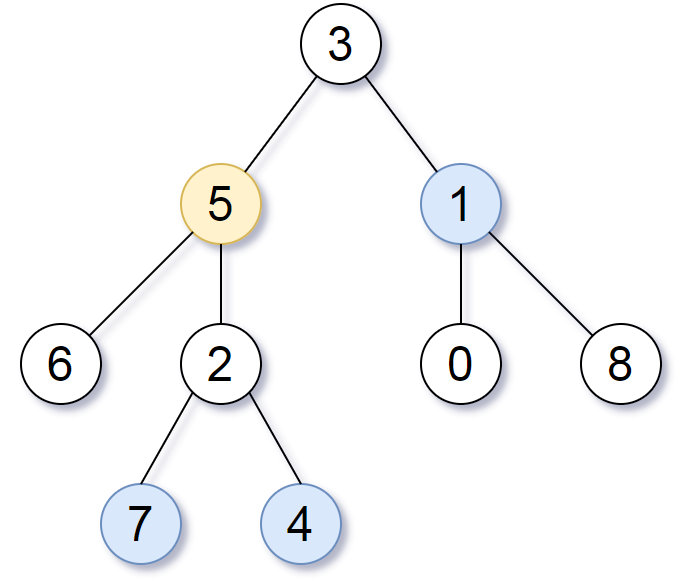
注意，输入的 "root" 和 "target" 实际上是树上的结点。 上面的输入仅仅是对这些对象进行了序列化描述。

提示：

1. 给定的树是非空的。
2. 树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
3. 目标结点 target 是树上的结点。
4. 0 <= K <= 1000.

思路分析：

• 可以使用深度优先遍历、也可以使用广度优先遍历；
• 重点是建立父亲结点和孩子结点的相互访问关系。

参考代码：

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class Solution {

    private Map<Integer, TreeNode> parents = new HashMap<>();
    private List<Integer> res = new ArrayList<>();

    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        // 从 root 出发 DFS，记录每个结点的父结点
        dfs1(root);

        // 从 target 出发 DFS，寻找所有深度为 k 的结点
        dfs2(target, null, 0, k);
        return res;
    }

    /**
     * 第 1 步：建立反向连接（从父亲结点可以访问子结点，也可以从子结点访问父亲结点）
     *
     * @param node
     */
    public void dfs1(TreeNode node) {
        // 无须对 node 做非空判断
        if (node.left != null) {
            parents.put(node.left.val, node);
            dfs1(node.left);
        }
        if (node.right != null) {
            parents.put(node.right.val, node);
            dfs1(node.right);
        }
    }

    /**
     * 第 2 步：进行深度优先遍历（事实上、广度优先遍历也可以）
     *
     * @param node
     * @param from 重点理解这里 from 的作用：只能遍历另外两个结点
     * @param depth
     * @param k
     */
    public void dfs2(TreeNode node, TreeNode from, int depth, int k) {
        if (node == null) {
            return;
        }
        if (depth == k) {
            res.add(node.val);
            return;
        }
        if (node.left != from) {
            dfs2(node.left, node, depth + 1, k);
        }
        if (node.right != from) {
            dfs2(node.right, node, depth + 1, k);
        }
        if (parents.get(node.val) != from) {
            dfs2(parents.get(node.val), node, depth + 1, k);
        }
    }
}

---

作者：liweiwei1419 链接：https://suanfa8.com/tree/solutions/0863-all-nodes-distance-k-in-binary-tree 来源：算法吧 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。